题目内容
10.已知函数f(x)=ex,g(x)=ln$\frac{x}{2}$+$\frac{1}{2}$的图象分别与直线y=m交于A,B两点,则|AB|的最小值为2+ln2.分析 由题意,求出A,B两点的坐标,表示|AB|,构造函数,确定函数的单调性,即可求出|AB|的最小值.
解答 解:由题意,A(lnm,m),B(2${e}^{m-\frac{1}{2}}$,m),其中2${e}^{m-\frac{1}{2}}$>lnm,且m>0,
∴|AB|=2${e}^{m-\frac{1}{2}}$-lnm,
设y=2${e}^{x-\frac{1}{2}}$-lnx(x>0),则y′=2${e}^{x-\frac{1}{2}}$-$\frac{1}{x}$,
令y′=0,解得x=$\frac{1}{2}$,
∴0<x<$\frac{1}{2}$时,y′<0;x>$\frac{1}{2}$时,y′>0,
∴y=-lnx(x>0)在(0,$\frac{1}{2}$)上单调递减,在($\frac{1}{2}$,+∞)上单调递增,
∴x=$\frac{1}{2}$时,|AB|min=2+ln2.
故答案为:2+2ln2.
点评 本题考查最值问题,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题

练习册系列答案
相关题目
18.把函数f(x)=sin(ωx+$\frac{π}{3}$)(ω>0)的图象向右平移$\frac{π}{6}$个单位后,得到函数g(x)的图象,若g(x)为偶函数,则ω的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.演绎推理“因为f′(x0)=0时,x0是f(x)的极值点.而对于函数f(x)=x3,f′(0)=0.所以0是函数f(x)=x3的极值点.”所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
 函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )
函数f(x)的定义域为(a,b),其导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在区间(a,b)内极小值点的个数是( )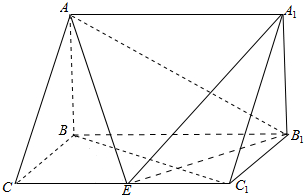 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.