题目内容
17.已知命题p:曲线$\frac{{x}^{2}}{a-3}$-$\frac{{y}^{2}}{6-a}$=1为双曲线,命题q:函数f(x)=x2-alnx在(2,3)上是增函数,若p∨(¬q)为假命题,求实数a的取值范围.分析 先根据双曲线的标准方程,函数导数符号和函数单调性的关系即可分别求出命题p,q为真时的a的取值范围,而由p∨(¬q)为假命题能得到p假q真,从而求p假时a的范围和q真时a的范围的交集即可.
解答 解:由命题p知,(a-3)(6-a)>0,∴3<a<6;
对于命题q,f′(x)=$\frac{2{x}^{2}-a}{x}$≥0在(2,3)上恒成立;
而y=2x2-a在(2,3)上是增函数;
∴只需2•22-a≥0,a≤8;
若p∨(¬q)为假命题,则p假q真;
∴3<a<6且a≤8;
∴实数a的取值范围为(3,6).
点评 考查双曲线的标准方程,函数导数符号和函数单调性的关系,二次函数的单调性,以及p∨q,¬q的真假和p,q真假的关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.设集合A={x|2≤x<4},B={x|3x-7≥8-2x},则A∪B等于( )
| A. | {x|3≤x<4} | B. | {x|x≥3} | C. | {x|x>2} | D. | {x|x≥2} |
5.演绎推理“因为f′(x0)=0时,x0是f(x)的极值点.而对于函数f(x)=x3,f′(0)=0.所以0是函数f(x)=x3的极值点.”所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
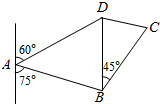 如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?
如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?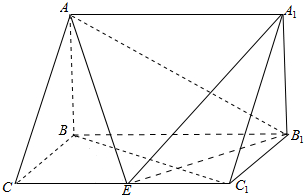 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.