题目内容
【题目】已知数列
的前
项和为
，且满足
.
（1）求数列的通项公式；
（2）求数列
的前
项和
．
【答案】（1）
；（2）
.
【解析】
试题分析：（1）利用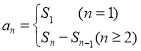
求得
，即为等比数列，进而求得；（2）由于数列是等差数列乘以等比数列，故采用错位相减求和法求得
.
试题解析：
（1）当
时，
，解得
；．．．．．．．．．．．．．．．．．．．．．．1分
当
时，
，两式相减得
，．．．．．．．．．．．．．．．3分
化简得，所以数列
是首项为1，公比为
的等比数列．
所以．．．．．．．．．．．．．．．．．．．．5分
（2）由（1）可得
，所以
，．．．．．．．．．．．．6分
【错位相减法】
．．．．．．．．．．．．．．．．8分
两式相减得
．．．．．．．．．．．．．．．．9分
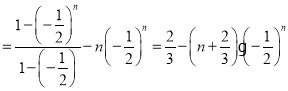，．．．．．．．．．．．．．．．．．．．11分
所以数列
的前
项和．．．．．．．．．．．．．．．．．12分
金牌课堂练系列答案
三新快车金牌周周练系列答案
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方
图：
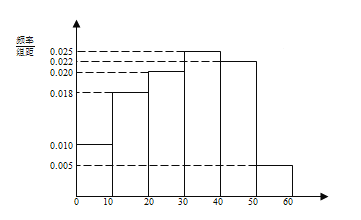
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
（Ⅰ）根据已知条件完成下面的
列联表，并据此资料，在犯错误的概率不超过
的前提下，你是否有理由认为“体育迷”与性别有关？
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
（Ⅱ）将上述调查所得到的频率视为概率，现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为
.若每次抽取的结果是相互独立的，求
的分布列，期望
和方差
.
附：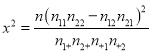 
|
|
|
|
|
|
【题目】为了了解某校学生喜欢吃辣是否与性别有关，随机对此校100人进行调查，得到如下的列表：已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为
．
喜欢吃辣 | 不喜欢吃辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
（1）请将上面的列表补充完整；
（2）是否有99.9%以上的把握认为喜欢吃辣与性别有关？说明理由：
下面的临界值表供参考：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：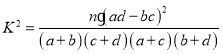
，其中
）