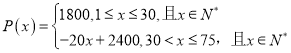题目内容
【题目】数列{an}中,a1=8,a4=2且满足an+2=2an+1-an(n∈N+)
(1)求数列{an}通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn
【答案】(1)an=10-2n(2)Sn=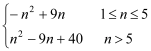
【解析】
试题分析:(1)由an+2=2an+1-an( n∈N*),变形为an+2-an+1=an+1-an,可知{ an }为等差数列,由已知利用通项公式即可得出.(2)由数列通项公式确定数列中的负数项和正数项,分情况去掉绝对值进行数列求和
试题解析:(1)由an+2=2an+1-an![]() an+2-an+1=an+1-an可知{an}成等差数列,
an+2-an+1=an+1-an可知{an}成等差数列,
d=![]() =-2,∴an=10-2n.
=-2,∴an=10-2n.
(2)由an=10-2n≥0可得n≤5,当n≤5时,Sn=-n2+9n,当n>5时,Sn=n2-9n+40,故Sn=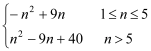

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目