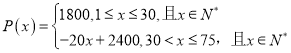Question

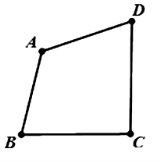
【题目】如图，在凸四边形中，为定点，,为动点，满足.

（1）写出与的关系式；

（2）设△BCD和△ABD的面积分别为和，求的最大值.

Answer 1

【答案】（1） （2）

【解析】

试题分析：（Ⅰ）在三角形BCD和三角形BCD中，利用余弦定理表示出BD2，两者相等表示即可得到cosC与cosA的关系式；（Ⅱ）利用三角形面积公式变形出S与T，进而表示出，将第一问表示出的cosA代入得到关于cosC的二次函数，利用二次函数性质即可求出的最大值

试题解析：（Ⅰ）连接BD，

∵CD=，AB=BC=DA=1，

∴在△BCD中，利用余弦定理得：BD2=BC2+CD2-2BCCDcosC=4-2cosC；

在△ABD中，BD2=2-2cosA，

∴4-2cosC=2-2cosA，

则cosA=cosC-1

（II）

…

由题意易知，,所以

当时，有最大值.