题目内容
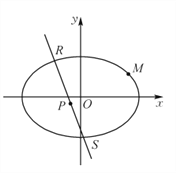
【题目】已知点A(x1,y1),D(x2,y2)其中(x1<x2)是曲线y2=9x(y≥0).上的两点,A,D两点在x轴上的射影分别为点B,C且|BC|=3.
(Ⅰ)当点B的坐标为(1,0)时,求直线AD的方程:
(Ⅱ)记△AOD的面积为S1,梯形ABCD的面积为S2,求![]() 的范围
的范围
【答案】(Ⅰ)y=x+2;(Ⅱ)![]() .
.
【解析】
(Ⅰ)根据![]() 和
和![]() 的横坐标相等即可求解
的横坐标相等即可求解![]() 的坐标,再求两点间的斜率利用点斜式求解即可.
的坐标,再求两点间的斜率利用点斜式求解即可.
(Ⅱ)设直线AD的方程为y=kx+m.联立直线与曲线的方程再表达出![]() 关于
关于![]() 的表达式,再根据直线与曲线的交点求出
的表达式,再根据直线与曲线的交点求出![]() 的范围进行求解即可.
的范围进行求解即可.
(Ⅰ)由B(1,0),可得A(1,y1),
代入y2=9x,得到y1=3,
又|BC|=3,则x2﹣x1=3,可得x2=4,
代入y2=9x,得到y2=6,
则kAD![]() 1,可得直线AD的方程为y﹣3=x﹣1,即y=x+2;
1,可得直线AD的方程为y﹣3=x﹣1,即y=x+2;
(Ⅱ)设直线AD的方程为y=kx+m.M(0,m),m>0,
则S1=S△OMD﹣S△OMA![]() .
.
由![]() ,得k2x2+(2km﹣9)x+m2=0,
,得k2x2+(2km﹣9)x+m2=0,
所以 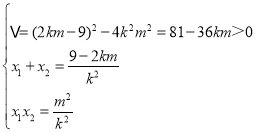 ,
,
又S2![]() (y1+y2)(x2﹣x1)
(y1+y2)(x2﹣x1)
所以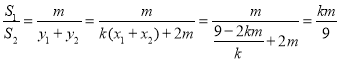
又注意到y1y2=3![]() 3
3![]() 0,所以k>0,m>0,
0,所以k>0,m>0,
因为△=81﹣36km>0,所以0<km![]() ,
,
所以![]() .
.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目