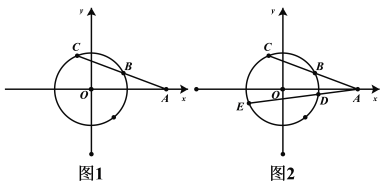
题目内容
【题目】在平面直角坐标系![]() 中,对于直线
中,对于直线![]() 和点
和点![]() 、
、![]() ,记
,记![]() ,若
,若![]() ,则称点
,则称点![]() ,
,![]() 被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点
被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点![]() ,
,![]() 被直线l分隔,则称直线l为曲线C的一条分隔线.
被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点![]() 、
、![]() 被直线
被直线![]() 分隔;
分隔;
(2)若直线![]() 是曲线
是曲线![]() 的分隔线,求实数
的分隔线,求实数![]() 的取值范围;
的取值范围;
(3)动点M到点![]() 的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
【答案】(1)证明见解析(2)![]() (3)
(3)![]() ,证明见解析
,证明见解析
【解析】
(1)根据点![]() ,
,![]() 被直线l分隔的定义证明即可,
被直线l分隔的定义证明即可,
(2)先由直线与曲线无交点,利用判别式小于0可得![]() 的范围,然后在曲线上取两个点验证是否被直线分隔,
的范围,然后在曲线上取两个点验证是否被直线分隔,
(3)先求出轨迹![]() 的方程,然后证明轨迹方程与
的方程,然后证明轨迹方程与![]() 轴无交点,再在轨迹
轴无交点,再在轨迹![]() 上取两个点验证是否被
上取两个点验证是否被![]() 轴分隔.
轴分隔.
(1)由题意得:![]() ,
,
![]() 被直线
被直线![]() 分隔;
分隔;
(2)由题意得:直线![]() 与曲线
与曲线![]() 无交点,
无交点,
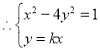 ,整理得
,整理得![]() 无解,即
无解,即![]()
![]() ,
,
又对任意的![]() ,点
,点![]() 和
和![]() 在曲线
在曲线![]() 上,满足
上,满足![]() ,所以点
,所以点![]() 和
和![]() 被直线
被直线![]() 分隔,
分隔,
![]() 所求的k的范围是
所求的k的范围是![]() .
.
(3)由题意得:设![]() ,
,![]() ,
,
化简得点M的轨迹方程为![]()
![]() 对任意的
对任意的![]() ,点
,点![]() 不是方程
不是方程![]() 的解
的解
![]() 直线
直线![]() 与曲线E没有交点,
与曲线E没有交点,
又曲线E上的两点![]() 和
和![]() 对于直线
对于直线![]() 满足
满足![]() ,
,
即点![]() 和
和![]() 被直线
被直线![]() 分隔,
分隔,
![]() 直线y轴是E的分隔线.
直线y轴是E的分隔线.

【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.