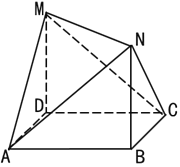
题目内容
【题目】将正方形![]() 沿对角线
沿对角线![]() 折起,当以
折起,当以![]() 四点为顶点的三棱锥体积最大时,异面直线
四点为顶点的三棱锥体积最大时,异面直线![]() 与
与![]() 所成的角为( )
所成的角为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:将正方形![]() 沿对角线
沿对角线![]() 折起,可得当三棱锥
折起,可得当三棱锥![]() 体积最大时,
体积最大时, ![]() 平面
平面![]() .设
.设![]() 是
是![]() 折叠前的位置,连接
折叠前的位置,连接![]() ,可得
,可得![]() 就算直线
就算直线![]() 与
与![]() 所成角,算出
所成角,算出![]() 的各边长,得
的各边长,得![]() 是等边三角形,从而求得直线
是等边三角形,从而求得直线![]() 与
与![]() 所成角的大小.
所成角的大小.
详解:设![]() 是正方形对角线
是正方形对角线![]() 、
、![]() 的交点,将正方形
的交点,将正方形![]() 沿对角线
沿对角线![]() 折起,
折起,
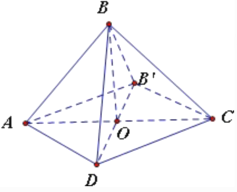
可得当![]() 平面
平面![]() 时,点
时,点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() ,而当
,而当![]() 与平面
与平面![]() 不垂直时,点
不垂直时,点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,且
,且![]() ,由此可得当三棱锥
,由此可得当三棱锥![]() 体积最大时,
体积最大时, ![]() 平面
平面![]() .设
.设![]() 是
是![]() 折叠前的位置,连接
折叠前的位置,连接![]() ,因为
,因为![]() ,所以
,所以![]() 就算直线
就算直线![]() 与
与![]() 所成角,设正方形的边长为
所成角,设正方形的边长为![]() ,因为
,因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
得![]() 是等边三角形,
是等边三角形, ![]() ,
,
所以直线![]() 与
与![]() 所成角为
所成角为![]() ,故选C.
,故选C.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目