题目内容
2.如图1,△ABC,AB=AC=4,$∠BAC=\frac{2π}{3}$,D为BC的中点,DE⊥AC,沿DE将△CDE折起至△C′DE,如图2,且C'在面ABDE上的投影恰好是E,连接C′B,M是C′B上的点,且$C'M=\frac{1}{2}MB$.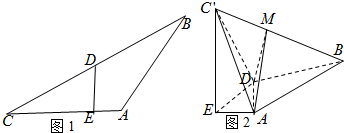
(1)求证:AM∥面C′DE;
(2)求三棱锥C′-AMD的体积.
分析 (1)要证AM∥面C′DE,可证AM所在的平面平行于面C′DE,结合已知过M作MN∥C'D,交BD于N,连接AN,利用面面平行的判定证明面AMN∥面C'DE;
(2)利用等积法把三棱锥C′-AMD的体积转化为$\frac{1}{2}$VB-AMD,进一步转化为M-ABD的体积求解.
解答 (1)证明:过M作MN∥C'D,交BD于N,连接AN,于是$DN=\frac{1}{2}NB$,
又AB=AC=4,$∠BAC=\frac{2π}{3}$,∴$B{C}^{2}={4}^{2}+{4}^{2}-2×4×4cos(\frac{2}{3}π)=48$,
∴BC=4$\sqrt{3}$,又D为BC的中点,
则DB=$2\sqrt{3}$,又$C′M=\frac{1}{2}MB$,
∴$NB=\frac{{4\sqrt{3}}}{3}$,∠B=$\frac{π}{6}$,由AN2=AB2+NB2-2AB•NB•cos$\frac{π}{6}$,得到$AN=\frac{{4\sqrt{3}}}{3}$,
∴∠ANB=$\frac{2}{3}π$,得AN∥ED,
∴面AMN∥面C'DE,即AM∥面C'DE;
(2)∵$C'M=\frac{1}{2}MB$,∴${V_{C'-AMD}}=\frac{1}{2}{V_{B-AMD}}=\frac{1}{2}{V_{M-ABD}}$,
又C′E⊥面ABD,∴M到平面ABD的距离h=2,${S_{△ABD}}=2\sqrt{3}$,
∴${V_{M-ABD}}=\frac{1}{3}×2×2\sqrt{3}=\frac{{4\sqrt{3}}}{3}$,即得三棱锥C′-AMD的体积为$\frac{{2\sqrt{3}}}{3}$.
点评 本题主要考查空间线面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案| A. | [-$\frac{\sqrt{3}}{2}$,0] | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{\sqrt{3}}{4}$,0] | D. | [-3,0] |
| A. | 命题是p∨q假命题 | B. | 命题是p∧q真命题 | ||
| C. | 命题是(?p)∨(?q)真命题 | D. | 命题是(?p)∧(?q)真命题 |
| A. | [$\frac{1}{2}$,$\frac{4}{3}$] | B. | [0,$\frac{1}{2}$] | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{4}{3}$] |
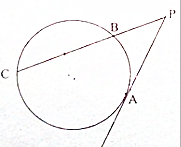 如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.
如图,PA是圆的切线,A为切点,PBC是圆的割线,且PB=$\frac{1}{2}$BC,则$\frac{PA}{PB}$=$\sqrt{3}$.