题目内容
10.设不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{2x-y≥0}\\{x-2≤0}\end{array}\right.$,表示的平面区域为D,若直线mx+y+m=0上存在区域D上的点,则实数m的取值范围是$-\frac{4}{3}≤m≤-\frac{1}{3}$.分析 由题意作出可行域,利用直线过定点,结合直线的斜率,求得满足直线mx+y+m=0上存在区域D上的点时的m的范围.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y-3≥0}\\{2x-y≥0}\\{x-2≤0}\end{array}\right.$作出可行域如图,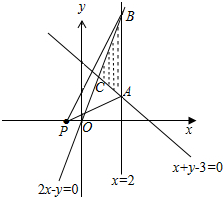
∵直线mx+y+m=0过定点P(-1,0),要使直线mx+y+m=0上存在区域D上的点,
则直线mx+y+m=0的斜率-m∈[kPA,kPB],
联立$\left\{\begin{array}{l}{x=2}\\{x+y-3=0}\end{array}\right.$,得A(2,1),
联立$\left\{\begin{array}{l}{x=2}\\{2x-y=0}\end{array}\right.$,得B(2,4),
∴${k}_{PA}=\frac{1-0}{2-(-1)}=\frac{1}{3}$,${k}_{PB}=\frac{4-0}{2-(-1)}=\frac{4}{3}$.
∴$\frac{1}{3}≤-m≤\frac{4}{3}$,即$-\frac{4}{3}≤m≤-\frac{1}{3}$.
故答案为$-\frac{4}{3}≤m≤-\frac{1}{3}$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法及数学转化思想方法,是中档题.

练习册系列答案
相关题目
1.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0,y≥0}\end{array}\right.$,则点(3,4)到点(x,y)的最小距离为( )
| A. | 3 | B. | $\sqrt{17}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
5.设f(x)为定义在R上的奇函数,且是周期为4的周期函数,f(1)=1,则f(-1)+f(8)=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
20.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=tanx | B. | y=2x | C. | y=x | D. | y=lg(1+x2) |
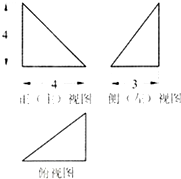 某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.
某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.