题目内容
11.已知直线y=kx+2与圆(x+2)2+(y-1)2=4相交于M,N两点,若|MN|≥2$\sqrt{3}$,则k的取值范围是( )| A. | [$\frac{1}{2}$,$\frac{4}{3}$] | B. | [0,$\frac{1}{2}$] | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{4}{3}$] |
分析 当弦长|MN|=2$\sqrt{3}$时,利用弦长公式求得弦心距d=1,故当|MN|≥2$\sqrt{3}$,则d≤1,由此求得k的范围.
解答 解:当弦长|MN|=2$\sqrt{3}$时,弦心距d=1
若|MN|≥2$\sqrt{3}$,则d≤1,
即圆心(-2,1)到直线kx-y+2=0的距离d=$\frac{|-2k-1+2|}{\sqrt{{k}^{2}+1}}$≤1,
求得k∈[0,$\frac{4}{3}$],
故选:D.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式、弦长公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0,y≥0}\end{array}\right.$,则点(3,4)到点(x,y)的最小距离为( )
| A. | 3 | B. | $\sqrt{17}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
20.下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A. | y=tanx | B. | y=2x | C. | y=x | D. | y=lg(1+x2) |
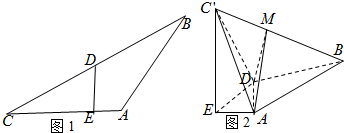
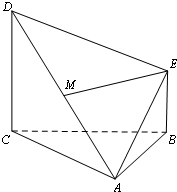 如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,
如图,多面体ABCDE中,CD⊥平面ABC,BE⊥平面ABC,AB=BC,BE=$\frac{1}{2}$CD,