题目内容
17．已知命题p：?x0∈R，sinx0=$\sqrt{2}$；命题q：?x∈R，x2-x+1＞0．则下列结论正确的是（ ）| A． | 命题是p∨q假命题 | B． | 命题是p∧q真命题 | ||
| C． | 命题是（?p）∨（?q）真命题 | D． | 命题是（?p）∧（?q）真命题 |
分析 首先判断命题p和q的真假，再利用真值表对照各选项选择．命题p的真假有正弦函数的有界性判断，命题q的真假结合二次函数的图象只需看△．
解答 解：命题p：因为-1≤sinx≤1，故不存在x∈R，使sinx=$\sqrt{2}$，命题p为假；
命题q：△=1-4=-3＜0，故?x∈R，都有x2+x+1＞0为真．
∴，命题是p∨q是真，命题“p∧q”是假命题，命题是（?p）∨（?q）真命题，命题是（?p）∧（?q）假命题．
故选：C
点评 本题考查命题和复合命题真假的判断、正弦函数的有界性及二次函数恒成立等知识，属基本题型的考查．
练习册系列答案
相关题目
在△ABC中，三个内角A，B，C的对边分别为a，b，c，其中c=2，且$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\frac{\sqrt{3}}{1}$．
5．设f（x）为定义在R上的奇函数，且是周期为4的周期函数，f（1）=1，则f（-1）+f（8）=（ ）
| A． | -2 | B． | -1 | C． | 0 | D． | 1 |
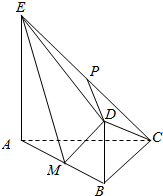如图，平面ABDE⊥平面ABC，AC⊥BC，AC=BC=4，四边形ABDE是直角梯形，BD∥AE，BD⊥BA，AE=2BD=4，P、M分别为CE，AB的中点．