题目内容
12．若{an}是一个各项都为正数的无穷递增等比数列，a1和a3是方程x2-5x+4=0的两个根，求此数列的通项公式an与前n项和Sn．分析 根据题意得出a1=1，a3=4，运用等比数列的性质求解q=2，即可得出通项公式，前n 项和．
解答 解：解方程得a1=1，a3=4，
设公比为q，由a3=a1q2得4=q2，q=2，
所以通项为an=a1qn-1=2n-1，
前n项和为Sn=$\frac{{a}_{1}（{q}^{n}-1）}{q-1}$=2n-1．
点评 本题考查数列的通项公式和前n项和公式的求法，解题时要注意等比数列和等差数列的性质的灵活运用，是中档题，解题时要认真审题，
练习册系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
4．
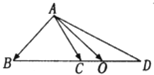在△ABC中，点D在线段BC的延长线上，且$\overrightarrow{BC}$=$\overrightarrow{CD}$，点O在线段CD上（点O与点C，D不重合），若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x的取值范围是（ ）
在△ABC中，点D在线段BC的延长线上，且$\overrightarrow{BC}$=$\overrightarrow{CD}$，点O在线段CD上（点O与点C，D不重合），若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$，则x的取值范围是（ ）| A． | （-1，0） | B． | （0，$\frac{1}{3}$） | C． | （0，1） | D． | （-$\frac{1}{3}$，0） |
1．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{x≥0，y≥0}\end{array}\right.$，则点（3，4）到点（x，y）的最小距离为（ ）
| A． | 3 | B． | $\sqrt{17}$ | C． | $\frac{3\sqrt{2}}{2}$ | D． | $\frac{2\sqrt{3}}{3}$ |
