题目内容
设函数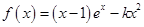 (其中
(其中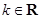 ).
).
(1) 当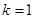 时,求函数
时,求函数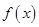 的单调区间;
的单调区间;
(2) 当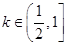 时,求函数
时,求函数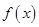 在
在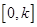 上的最大值
上的最大值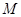 .
.
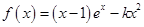 (其中
(其中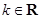 ).
).(1) 当
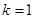 时,求函数
时,求函数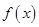 的单调区间;
的单调区间;(2) 当
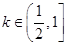 时,求函数
时,求函数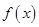 在
在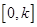 上的最大值
上的最大值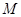 .
.(1) 函数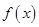 的递减区间为
的递减区间为 ,递增区间为
,递增区间为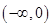 ,
,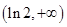 ;
;
(2)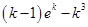
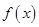 的递减区间为
的递减区间为 ,递增区间为
,递增区间为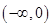 ,
,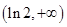 ;
; (2)
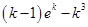
试题分析:(1)由
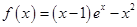
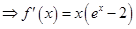 ,利用导数的符号判断函数
,利用导数的符号判断函数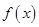 的单调性和求单调区间;
的单调性和求单调区间;(2)
试题解析:
解:(1)当
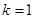 时,
时,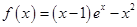 ,
,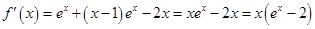
令
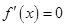 ,得
,得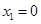 ,
,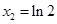
当
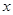 变化时,
变化时,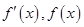 的变化如下表:
的变化如下表: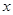 | 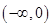 |  |  | 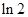 | 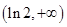 |
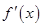 | 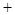 |  | 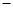 |  | 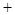 |
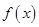 | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
右表可知,函数
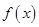 的递减区间为
的递减区间为 ,递增区间为
,递增区间为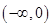 ,
,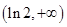 .
. (2)
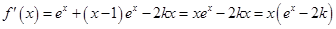 ,令
,令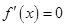 ,得
,得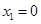 ,
,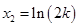 , 令
, 令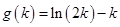 ,则
,则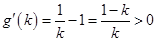 ,所以
,所以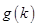 在
在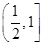 上递增, 所以
上递增, 所以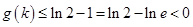 ,从而
,从而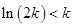 ,所以
,所以
所以当
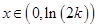 时,
时,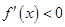 ;当
;当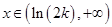 时,
时,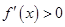 ;
;所以
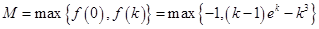
令
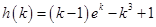 ,则
,则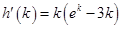 ,令
,令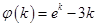 ,则
,则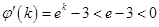
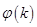 在
在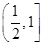 上递减,而
上递减,而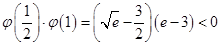
所以存在
 使得
使得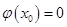 ,且当
,且当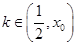 时,
时,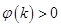 当
当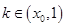 时,
时,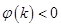
所以
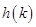 在
在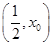 上单调递增,在
上单调递增,在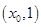 上单调递减.
上单调递减.因为
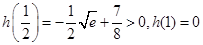 ,所以
,所以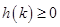 在
在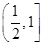 上恒成立,当且仅当
上恒成立,当且仅当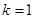 时取得“=”.综上,函数
时取得“=”.综上,函数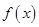 在
在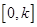 上的最大值
上的最大值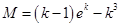 .
.
练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
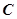 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积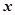 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是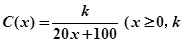 为常数).记
为常数).记 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.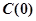 的实际意义,并建立
的实际意义,并建立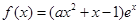 ,其中
,其中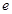 是自然对数的底数,
是自然对数的底数, .
. ,求曲线
,求曲线 在点
在点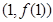 处的切线方程;
处的切线方程; ,求
,求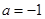 ,函数
,函数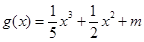 的图像有3个不同的交点,求实数
的图像有3个不同的交点,求实数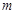 的取值范围.
的取值范围. 在区间
在区间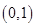 上单调递增,且方程
上单调递增,且方程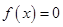 的根都在区间
的根都在区间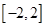 上,则实数b的取值范围为( )
上,则实数b的取值范围为( )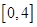

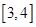
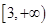
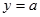 与函数
与函数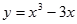 的图像有三个相异的交点,则
的图像有三个相异的交点,则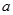 的取值范围为( )
的取值范围为( )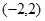
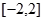
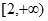

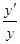 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)· ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·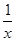 的单调递增区间是________.
的单调递增区间是________.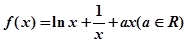
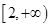 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.