题目内容
我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得ln y=φ(x)lnf(x),两边求导得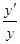 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)· ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)· ].运用此方法可以探求得y=x
].运用此方法可以探求得y=x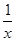 的单调递增区间是________.
的单调递增区间是________.
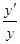 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)· ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)· ].运用此方法可以探求得y=x
].运用此方法可以探求得y=x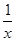 的单调递增区间是________.
的单调递增区间是________.(0,e)
由题意知y′=x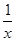 (-
(-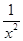 ln x+
ln x+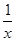 ·
·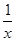 )
)
=x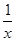 ·
·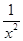 (1-ln x),x>0,
(1-ln x),x>0,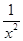 >0,x
>0,x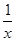 >0,
>0,
令y′>0,则1-ln x>0,所以0<x<e.
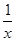 (-
(-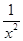 ln x+
ln x+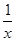 ·
·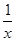 )
)=x
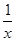 ·
·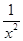 (1-ln x),x>0,
(1-ln x),x>0,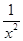 >0,x
>0,x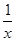 >0,
>0,令y′>0,则1-ln x>0,所以0<x<e.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
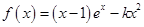 (其中
(其中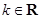 ).
).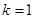 时,求函数
时,求函数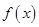 的单调区间;
的单调区间;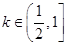 时,求函数
时,求函数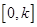 上的最大值
上的最大值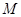 .
.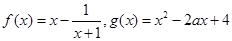 若对任意x1∈[0,1],存在x2∈[1,2],使
若对任意x1∈[0,1],存在x2∈[1,2],使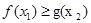 ,求实数a的取值范围?
,求实数a的取值范围?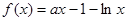 (
(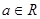 )
)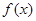 的单调性;
的单调性;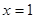 处取得极值,不等式
处取得极值,不等式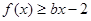 对任意
对任意 恒成立,求实数
恒成立,求实数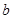 的取值范围;
的取值范围;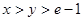 时,证明不等式
时,证明不等式 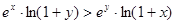 .
.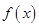 =
=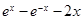 .
.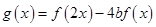 ,当
,当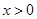 时,
时,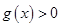 ,求
,求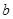 的最大值;
的最大值;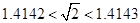 ,估计ln2的近似值(精确到0.001)
,估计ln2的近似值(精确到0.001)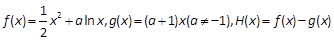 。
。 的单调减区间是
的单调减区间是 ,求实数a的值;
,求实数a的值;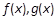 在区间
在区间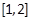 上都为单调函数且它们的单调性相同,求实数a的取值范围;
上都为单调函数且它们的单调性相同,求实数a的取值范围;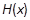 的两个极值点,a<b,
的两个极值点,a<b,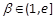 。求证:对任意的
。求证:对任意的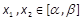 ,不等式
,不等式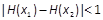 成立.
成立. 在
在 时取得极小值.
时取得极小值. 的值;
的值; ,使得
,使得 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.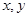 轴上滑动,点M在线段AB上,且
轴上滑动,点M在线段AB上,且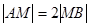 ,
,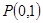 的直线
的直线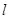 与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求
与曲线C交于不同两点E、F,N是曲线上不同于E、F的动点,求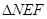 面积的最大值.
面积的最大值.