题目内容
15.若抛物线y=x2与以(0,1)为圆心,r为半径的圆相交于A、B、C、D四个点,则r的取值范围为($\frac{\sqrt{3}}{2}$,1).分析 先联立抛物线与圆的方程消去x,得到y的二次方程,根据抛物线与圆相交于A、B、C、D四个点的充要条件是此方程有两个不相等的正根,可求出r的范围.
解答 解:将抛物线y=x2代入圆x2+(y-1)2=r2(r>0)的方程,
消去x2,整理得y2-y+1-r2=0(1)
抛物线与圆相交于A、B、C、D四个点的充要条件是:
方程(1)有两个不相等的正根
∴$\left\{\begin{array}{l}1-4(1-{r}^{2})>0\\ 1-{r}^{2}>0\\ r>0\end{array}\right.$.
解得r∈($\frac{\sqrt{3}}{2}$,1),
故r的取值范围为($\frac{\sqrt{3}}{2}$,1),
故答案为:($\frac{\sqrt{3}}{2}$,1)
点评 本题主要考查抛物线和圆的综合问题.圆锥曲线是高考必考题,要强化复习.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.已知甲、乙两名同学高三一年10次数学测试成绩的茎叶图如图所示,则下列说法正确的是( )
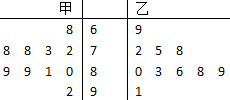

| A. | 甲同学的平均成绩高于乙同学的平均成绩 | |
| B. | 甲同学成绩的中位数大于乙同学成绩的中位数 | |
| C. | 甲同学的成绩要比乙同学的成绩稳定 | |
| D. | 乙同学的成绩要比甲同学的成绩稳定 |