题目内容
5.求下列数列的通项公式:(1)a1=1,an=$\sqrt{3{{a}_{n-1}}^{2}}$(n≥2);
(2)a1=1,an+1-an=kan•an+1.
分析 (1)通过an=$\sqrt{3{{a}_{n-1}}^{2}}$>0可知${{a}_{n}}^{2}$=3${{a}_{n-1}}^{2}$,进而数列{${{a}_{n}}^{2}$}是以1为首项、3为公比的等比数列,计算即得结论;
(2)通过对等式an+1-an=kan•an+1两边同时除以kan•an+1可知$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$=k,进而数列{$\frac{1}{{a}_{n}}$}是以1为首项、-k为公差的等差数列,计算即得结论.
解答 解:(1)∵an=$\sqrt{3{{a}_{n-1}}^{2}}$>0,
∴${{a}_{n}}^{2}$=3${{a}_{n-1}}^{2}$,
又∵${{a}_{1}}^{2}$=1,
∴数列{${{a}_{n}}^{2}$}是以1为首项、3为公比的等比数列,
∴${{a}_{n}}^{2}$=3n-1,
∴an=$\sqrt{{3}^{n-1}}$=${3}^{\frac{n-1}{2}}$;
(2)∵an+1-an=kan•an+1,
∴$\frac{{a}_{n+1}-{a}_{n}}{{a}_{n+1}•{a}_{n}}$=$\frac{k{a}_{n}•{a}_{n+1}}{{a}_{n}•{a}_{n+1}}$,即$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n+1}}$=k,
又∵$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项、-k为公差的等差数列,
∴$\frac{1}{{a}_{n}}$=1-(n-1)k,
∴an=$\frac{1}{1-(n-1)k}$.
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.

| A. | $\sqrt{13}$ | B. | 17 | C. | $\frac{53}{4}$ | D. | $\frac{\sqrt{53}}{2}$ |
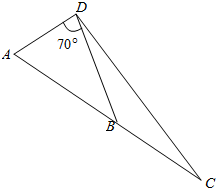 为保障行车安全,有关方面决定自2015年3月14日起,对开通至今已27年延安东路隧道进行封闭大修.如图所示,A点是延安东路隧道浦东入口处,B点是人民隧道入口处,C点是复兴东路隧道入口处,A、B、C三点可近似看成在一条直线上.已知AB间距离约为1.2km,BC间距离约为0.8km.现在有一车辆在银城浦东南路路口的D点处此路口到A点的距离约为0.8km,此处连接A点与B点的线段张角为70°.请问这个路口到复兴东路隧道入口的距离约为多少千米?(结果精确到0.1km)
为保障行车安全,有关方面决定自2015年3月14日起,对开通至今已27年延安东路隧道进行封闭大修.如图所示,A点是延安东路隧道浦东入口处,B点是人民隧道入口处,C点是复兴东路隧道入口处,A、B、C三点可近似看成在一条直线上.已知AB间距离约为1.2km,BC间距离约为0.8km.现在有一车辆在银城浦东南路路口的D点处此路口到A点的距离约为0.8km,此处连接A点与B点的线段张角为70°.请问这个路口到复兴东路隧道入口的距离约为多少千米?(结果精确到0.1km)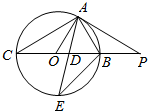 如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.
如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.