题目内容
6.已知a,b,c>0,求$\frac{a+3c}{a+2b+c}+\frac{4b}{a+b+2c}-\frac{8c}{a+b+3c}$的最小值,并求此时的a,b,c.分析 a+2b+c=x,a+b+2c=y,a+b+3c=z,(x,y,z>0),则c=z-y,b=x+z-2y,a=5y-3z-x,化简可得原式,再由基本不等式可得最小值,求得等号成立的条件.
解答 解:设a+2b+c=x,a+b+2c=y,a+b+3c=z,(x,y,z>0),
则c=z-y,b=x+z-2y,a=5y-3z-x,
则原式=$\frac{2y-x}{x}$+$\frac{4(x+z-2y)}{y}$-$\frac{8(z-y)}{z}$
=($\frac{2y}{x}$+$\frac{4x}{y}$)+($\frac{4z}{y}$+$\frac{8y}{z}$)-17
≥2$\sqrt{\frac{2y}{x}•\frac{4x}{y}}$+2$\sqrt{\frac{4z}{y}•\frac{8y}{z}}$-17
=12$\sqrt{2}$-17.
当且仅当$\frac{2y}{x}$=$\frac{4x}{y}$,$\frac{4z}{y}$=$\frac{8y}{z}$即为y=$\sqrt{2}$x,z=$\sqrt{2}$y,
即有a=($\sqrt{2}$-1)b,c=($\sqrt{2}$+2)b取得最小值,
且为12$\sqrt{2}$-17.
点评 本题考查换元法和化简整理的能力,同时考查基本不等式的运用:求最值,属于中档题.

练习册系列答案
相关题目
11.在△ABC中,已知(b+c):(c+a):(a+b)=4:5:6,则sinA:sinB:sinC等于( )
| A. | 6:5:4 | B. | 7:5:3 | C. | 3:5:7 | D. | 4:5:6 |
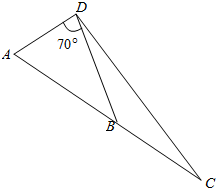 为保障行车安全,有关方面决定自2015年3月14日起,对开通至今已27年延安东路隧道进行封闭大修.如图所示,A点是延安东路隧道浦东入口处,B点是人民隧道入口处,C点是复兴东路隧道入口处,A、B、C三点可近似看成在一条直线上.已知AB间距离约为1.2km,BC间距离约为0.8km.现在有一车辆在银城浦东南路路口的D点处此路口到A点的距离约为0.8km,此处连接A点与B点的线段张角为70°.请问这个路口到复兴东路隧道入口的距离约为多少千米?(结果精确到0.1km)
为保障行车安全,有关方面决定自2015年3月14日起,对开通至今已27年延安东路隧道进行封闭大修.如图所示,A点是延安东路隧道浦东入口处,B点是人民隧道入口处,C点是复兴东路隧道入口处,A、B、C三点可近似看成在一条直线上.已知AB间距离约为1.2km,BC间距离约为0.8km.现在有一车辆在银城浦东南路路口的D点处此路口到A点的距离约为0.8km,此处连接A点与B点的线段张角为70°.请问这个路口到复兴东路隧道入口的距离约为多少千米?(结果精确到0.1km)