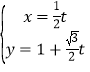题目内容
【题目】在△ABC中，角A，B，C的对边分别为a，b，c，已知2（tanA+tanB）= 
．
（1）证明：a+b=2c；
（2）求cosC的最小值．
【答案】
（1）
证明：由2（tanA+tanB）= 
得：
；
∴两边同乘以cosAcosB得，2（sinAcosB+cosAsinB）=sinA+sinB；
∴2sin（A+B）=sinA+sinB；
即sinA+sinB=2sinC（1）；
根据正弦定理， 
；
∴ 
， 
, 
，带入（1）得： 
；
∴a+b=2c；
（2）
解：a+b=2c；
∴（a+b）2=a2+b2+2ab=4c2；
∴a2+b2=4c2﹣2ab，且4c2≥4ab，当且仅当a=b时取等号；
又a，b＞0；
∴ 
；
∴由余弦定理， 
= 
；
∴cosC的最小值为 
【解析】（1）由切化弦公式 
，带入 
并整理可得2（sinAcosB+cosAsinB）=sinA+cosB，这样根据两角和的正弦公式即可得到sinA+sinB=2sinC，从而根据正弦定理便可得出a+b=2c；
（2）根据a+b=2c，两边平方便可得出a2+b2+2ab=4c2 ， 从而得出a2+b2=4c2﹣2ab，并由不等式a2+b2≥2ab得出c2≥ab，也就得到了 ，这样由余弦定理便可得出 
，从而得出cosC的范围，进而便可得出cosC的最小值．
考查切化弦公式，两角和的正弦公式，三角形的内角和为π，以及三角函数的诱导公式，正余弦定理，不等式a2+b2≥2ab的应用，不等式的性质．
【考点精析】根据题目的已知条件，利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:
；余弦定理:
;
;
．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
