题目内容
【题目】在平面直角坐标系xOy中，以O为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ＝2(cos θ＋sin θ)．
(1)求C的直角坐标方程；
(2)直线l：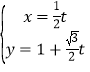
(t为参数)与曲线C交于A，B两点，与y轴交于点E，求|EA|＋|EB|.
【答案】(1)(x－1)2＋(y－1)2＝2;(2)
.
【解析】试题分析：（1）根据极坐标和直角坐标互化的公式得到直角坐标；（2）将直线参数方程和曲线联立得到二次方程，因为|EA|＋|EB|＝|t1|＋|t2|＝|t1－t2|，由弦长公式得到结果.
解析：
(1)由ρ＝2(cos θ＋sin θ)得ρ2＝2ρ(cos θ＋sin θ)，
所以曲线C的直角坐标方程为x2＋y2＝2x＋2y，
即(x－1)2＋(y－1)2＝2.
(2)将l的参数方程代入曲线C的直角坐标方程，
化简得t2－t－1＝0，
点E对应的参数t＝0，
设点A，B对应的参数分别为t1，t2，
则t1＋t2＝1，t1t2＝－1，
所以|EA|＋|EB|＝|t1|＋|t2|＝|t1－t2|
＝
＝
.
练习册系列答案
相关题目
