题目内容
7. 如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
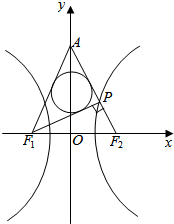
如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
分析 本题先根据直角三角形内切圆半径得到边长的关系,结合双曲线定义和图形的对称必,求出a的值,由|F1F2|=2,求出c的值,从而得到双曲线的离心率,得到本题结论.
解答 :∵PF1⊥PF2,△APF1的内切圆半径为$\frac{1}{2}$,
∴|PF1|+|PA|-|AF1|=1,
∴|PF2|+2a+|PA|-|AF1|=1,
∴|AF2|-|AF1|=1-2a,
∵由图形的对称性知:|AF2|=|AF1|,
∴a=$\frac{1}{2}$.
∵|F1F2|=2,
∴c=1,
∴e=$\frac{c}{a}$=2.
故答案为:2.
点评 本题考查了双曲线的定义、图形的对称性,本题难度不大,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
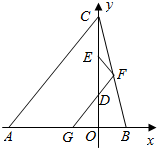 如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.
如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.