题目内容
17.使x2-2ax+2≥a恒成立的a是否存在?若存在,求出a;若不存在,说明理由.分析 由题意可得不等式x2-2ax+2-a≥0恒成立,由判别式△=4a2-4(2-a)≤0,解不等式即可得到a的范围.
解答 解:x2-2ax+2≥a恒成立
即为x2-2ax+2-a≥0恒成立,
由判别式△=4a2-4(2-a)≤0,
即a2+a-2≤0,
解得-2≤a≤1.
则存在a,且-2≤a≤1.使x2-2ax+2≥a恒成立.
点评 本题考查不等式恒成立问题的解法,注意运用二次函数的图形和性质,考查运算能力,属于基础题.

练习册系列答案
相关题目
8.已知直线l的方程是y=k(x-1)-2,若点P(-3,0)在直线l上的射影为H,O为坐标原点,则|OH|的最大值是( )
| A. | 5+$\sqrt{2}$ | B. | 3+2$\sqrt{2}$ | C. | $\sqrt{5}+\sqrt{2}$ | D. | $\sqrt{3}+3\sqrt{2}$ |
12.不等式|x-a|<b的解集是{x|-3<x<9},则a,b的值分别是( )
| A. | a=3,b=6 | B. | a=-3,b=9 | C. | a=6,b=3 | D. | a=-3,b=6 |
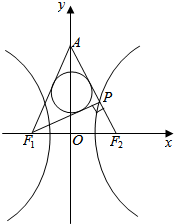 如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.