题目内容
6.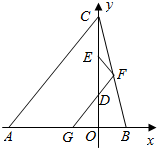 如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.
如图,△ABC的三个顶点坐标分别为A(-6,0),B(2,0),C(0,6),D,E分别是高CO的两个三等分点,过D,作直线FG∥AC,分别交AB和BC于G,F,连接EF.(1)求过E,G,F三点的圆M的方程;
(2)在线段AC上是否存在点H,使得过点H存在和圆M相切的直线,并且若过点H存在两条切线时,则点H和两切点P,Q组成的∠PHQ≥90°?若存在,求出H点对应轨迹的长度;若不存在,试说明理由.
分析 (1)判断EG是△EFG的斜边,即可求出过E,G,F三点的圆M的方程;
(2)点在圆M外时,过点H存在两条切线,由点H和两切点P,Q组成的∠PHQ≥90°,得直角△HPM的一个锐角∠PHM≥45°,于是HM≤$\sqrt{2}$PM=$\sqrt{2}$r,即HM≤$\sqrt{10}$.设H(x,x+6)(-6≤x≤0),确定H的横坐标的范围,即可得出结论.
解答 解:(1)由题意,G(-2,0),E(0,4),F(1,3),
∴EF=$\sqrt{2}$,EG=$\sqrt{20}$,FG=$\sqrt{18}$,
∴EF2+FG2=EG2,
∴EG是△EFG的斜边,
∴过E,G,F三点的圆M的方程为(x+1)2+(y-2)2=5;
(2)假设线段AC上存在点H,则H在圆上或圆外.
点在圆M外时,过点H存在两条切线,由点H和两切点P,Q组成的∠PHQ≥90°,得直角△HPM的一个锐角∠PHM≥45°,于是HM≤$\sqrt{2}$PM=$\sqrt{2}$r,即HM≤$\sqrt{10}$.
∵H在线段AC:y=x+6(-6≤x≤0)上,
∴设H(x,x+6)(-6≤x≤0),
由HM2=(x+1)2+(x+6-2)2≤10,得$\frac{-5-\sqrt{11}}{2}$≤x≤$\frac{-5+\sqrt{11}}{2}$,满足-6≤x≤0,
此时线段AC上满足$\frac{-5-\sqrt{11}}{2}$≤x≤$\frac{-5+\sqrt{11}}{2}$的点对应的线段长度为$\frac{\sqrt{22}}{2}$;
∵圆心M(-1,2)到线段AC的距离d=$\frac{|-1-2+6|}{\sqrt{2}}$=$\frac{3}{\sqrt{2}}$,
∴直线AC被圆M截得的弦长为2$\sqrt{5-\frac{9}{2}}$=$\sqrt{2}$,
∴H点对应轨迹的长度为$\frac{\sqrt{22}}{2}$-$\sqrt{2}$.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

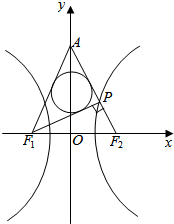 如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.