题目内容
19.设函数y=f(x)在(a,b)上的导函数f′(x),f′(x)在(a,b)上的导函数为f″(x).若在(a,b)上,f″(x)>0恒成立,则称函数y=f(x)在(a,b)上为“凹函数”.若f(x)=-$\frac{1}{6}$x3+x2-aex+2是R上的“凹函数”,求实数a的取值范围.分析 求函数导数,结合导数不等式进行求解,构造函数,利用导数研究函数的极值和最值即可.
解答 解:∵f(x)=-$\frac{1}{6}$x3+x2-aex+2,
∴函数的导数f′(x)=-$\frac{1}{2}$x2+2x-aex,
f′′(x)=-x+2-aex,
∵f(x)=-$\frac{1}{6}$x3+x2-aex+2是R上的“凹函数”,
∴f″(x)>0恒成立,
即f″(x)=-x+2-aex>0恒成立,
即aex<2-x,
即a<$\frac{2-x}{{e}^{x}}$,
设h(x)=$\frac{2-x}{{e}^{x}}$,
则h′(x)=$\frac{-{e}^{x}-(2-x){e}^{x}}{({e}^{x})^{2}}$=$\frac{x-3}{{e}^{x}}$,
由h′(x)>0得x>3,此时函数单调递增,由h′(x)<0,得x<3,此时函数递减,
故当x=3时,函数h(x)取得极小值同时也是最小值h(3)=$\frac{2-3}{{e}^{3}}$=-$\frac{1}{{e}^{3}}$,
则h(x)=$\frac{2-x}{{e}^{x}}$≥-$\frac{1}{{e}^{3}}$,
故a<-$\frac{1}{{e}^{3}}$,
即a的取值范围是(-∞,-$\frac{1}{{e}^{3}}$).
点评 本题主要考查导数的综合应用,求函数的导数,构造函数,利用导数研究函数的极值和最值是解决本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
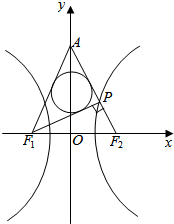 如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.
如图,F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,且|F1F2|=2.若双曲线C的右支上存在点P,使得PF1⊥PF2.设直线PF2与y轴交于点A,且△APF1的内切圆半径为$\frac{1}{2}$,则双曲线C的离心率为2.