题目内容
15．在△ABC中，c=3，b=$\sqrt{3}$，C=120°，解三角形．分析 利用正弦定理求出B，然后求解A，利用三角形的形状求解c即可．
解答 解：在△ABC中，c=3，b=$\sqrt{3}$，C=120°，
由正弦定理可得：sinB=$\frac{bsinC}{c}$=$\frac{\sqrt{3}×\frac{\sqrt{3}}{2}}{3}$=$\frac{1}{2}$，
∴B=30°，可得A=180°-120°-30°=30°．
由于三角形的等腰三角形，可得a=$\sqrt{3}$．
点评 本题考查三角形的解法，正弦定理的应用，考查计算能力．
练习册系列答案
相关题目
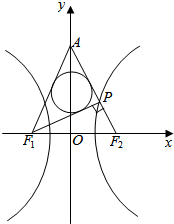如图，F1，F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，且|F1F2|=2．若双曲线C的右支上存在点P，使得PF1⊥PF2．设直线PF2与y轴交于点A，且△APF1的内切圆半径为$\frac{1}{2}$，则双曲线C的离心率为2．