��Ŀ����
1����֪$\overrightarrow{a}$=��x+1��y����$\overrightarrow{b}$=��x-1��y��������x��y��R����|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=4������P��x��y���Ĺ켣ΪL��������P��x��y���Ĺ켣���̣�
������֪��F1��-1��0��������F2��1��0����ֱ��l��켣L�ཻ��A��B���㣬�ʡ�ABF1������Բ������Ƿ�������ֵ�������ڣ����������ֵ��ֱ��l�ķ��̣��������ڣ���˵�����ɣ�
���� ����ֱ������֪���|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=4����ö���P��x��y���Ĺ켣���̣�
���ѡ�ABF1������Բ��������ת��Ϊ��ABF1�����������ֱ��l�ķ���Ϊx=my+1������ֱ�߷��̺���Բ���̣�ת��Ϊ����y��һԪ���η��̣��ɺ����ĵ��������ʹ��ABF1���������mֵ����һ���������Բ��������ֵ��
��� �⣺������$\overrightarrow{a}$=��x+1��y����$\overrightarrow{b}$=��x-1��y������|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=4��
�ã�$\sqrt{��x+1��^{2}+{y}^{2}}+\sqrt{��x-1��^{2}+{y}^{2}}=4$��
�����ã�$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$��
��������ABF1������Բ������������Բ�İ뾶���
�ߡ�ABF1���ܳ�Ϊ��Բ$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$�ij��᳤��2��Ϊ��ֵ��
���ABF1��������
��ֱ��l�ķ���Ϊx=ty+1��
����$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{x=my+1}\end{array}\right.$�����3m2+4��y2+6my-9=0��
��A��x1��y1����B��x2��y2����
��${y}_{1}+{y}_{2}=-\frac{6m}{3{m}^{2}+4}��{y}_{1}{y}_{2}=-\frac{9}{3{m}^{2}+4}$��
��$|{y}_{1}-{y}_{2}|=\sqrt{��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{��-\frac{6m}{3{m}^{2}+4}��^{2}-4����-\frac{9}{3{m}^{2}+4}��}$
=$\sqrt{\frac{36{m}^{2}+36��3{m}^{2}+4��}{��3{m}^{2}+4��^{2}}}$=$\sqrt{\frac{144��{m}^{2}+1��}{[3��{m}^{2}+1��+1]^{2}}}$=$\sqrt{\frac{144}{9��{m}^{2}+1��+\frac{1}{{m}^{2}+1}+6}}$��
��m2+1=1����m=0ʱ��|y1-y2|max=3��
��ʱ��ABF1�����������ֵΪ$\frac{1}{2}��2��3=3$��
���ABF1������Բ�İ뾶Ϊr����$\frac{1}{2}��4��2r=3$��r=$\frac{3}{4}$��
����Բ�����Ϊ$\frac{9}{16}��$����ʱֱ��l�ķ���Ϊx=1��
���� ���⿼����ƽ�����������ߵĹ켣���̣�������ֱ�ߺ�Բ���ߵ�λ�ù�ϵ������������������иߵ��⣮

| A�� | ��0��1�� | B�� | ��-1��3�� | C�� | ��1��1�� | D�� | ��-1��1�� |
| A�� | 62.8��3.6 | B�� | 62.8��14.4 | C�� | 65.6��3.6 | D�� | 65.6��14.4 |
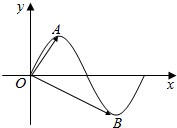 ��֪����f��x��=$\sqrt{3}$sin��x���أ�0���IJ���ͼ����ͼ��ʾ��A��B�ֱ����ⲿ��ͼ���ϵ���ߵ㡢��͵㣬OΪ����ԭ�㣬��$\overrightarrow{OA}$•$\overrightarrow{OB}$=0������f��x+1���ǣ�������
��֪����f��x��=$\sqrt{3}$sin��x���أ�0���IJ���ͼ����ͼ��ʾ��A��B�ֱ����ⲿ��ͼ���ϵ���ߵ㡢��͵㣬OΪ����ԭ�㣬��$\overrightarrow{OA}$•$\overrightarrow{OB}$=0������f��x+1���ǣ�������| A�� | ����Ϊ4���溯�� | B�� | ����Ϊ4��ż���� | ||
| C�� | ����Ϊ2�е��溯�� | D�� | ����Ϊ2�е�ż���� |
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{2}$ |