题目内容
1.存在实数a,使得对函数y=g(x)定义域内的任意x,都有a<g(x)成立,则称a为g(x)的下界,若a为所有下界中最大的数,则称a为函数g(x)的下确界.已知x,y,z∈R+且以x,y,z为边长可以构成三角形,则f(x,y,z)=$\frac{xy+yz+zx}{{{{({x+y+z})}^2}}}$的下确界为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 运用极端法,就是三角形在趋近于无法构成时,即:x→0,并令y=z,可得原式>$\frac{1}{4}$恒成立,再由分析法证明,注意运用配方和三角形的三边关系,可得下确界为$\frac{1}{4}$.
解答 解:运用极端法,就是三角形在趋近于无法构成时,
即:x→0,并令y=z,
所以$\frac{xy+yz+zx}{(x+y+z)^{2}}$=$\frac{1}{4}$,当然此值只是一个极限值,
原式=$\frac{xy+yz+zx}{(x+y+z)^{2}}$>$\frac{1}{4}$恒成立,
可运用分析法证明上式.
即证(x+y+z)2<4xy+4yz+4zx,
即有x2+y2+z2<2xy+2yz+2zx,
即有(x-y)2+(y-z)2+(z-x)2<x2+y2+z2,
由三角形中,|x-y|<z,|y-z|<x,|z-x|<y,
均为(x-y)2<z2,(y-z)2<x2,(z-x)2<y2.
则上式成立.
故下确界是$\frac{1}{4}$.
故选B.
点评 本题考查新定义的理解和运用,考查三角形的三边的关系和不等式的证明,属于中档题.

练习册系列答案
相关题目
6.下列函数中,值域为[-2,2]的是( )
| A. | f(x)=2x-1 | B. | f(x)=log0.5(x+11) | C. | f(x)=$\frac{4x}{{x}^{2}+1}$ | D. | f(x)=x2(4-x2) |
13.已知定义在R上的奇函数f(x)=$\frac{ax+b}{{x}^{2}+c}$的图象如图所示,则a,b,c的大小关系是( )
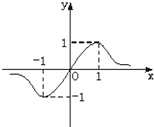

| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | a>c>b |
10.设随机变量X的概率分布如右下,则P(X≥0)=( )
| X | -1 | 0 | 1 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | p |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |