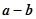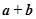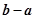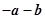题目内容
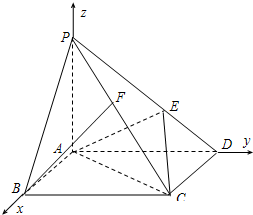
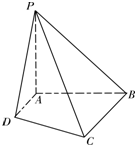
如图,在底面是正方形的四棱锥P-ABCD中,PA=AB=1,PB=PD=
,点E在PD上,且PE:ED=2:1.
(1)求证:PA⊥平面ABCD;
(2)求二面角D-AC-E的余弦值;
(3)在棱PC上是否存在一点F,使得BF∥平面ACE.

| 2 |
(1)求证:PA⊥平面ABCD;
(2)求二面角D-AC-E的余弦值;
(3)在棱PC上是否存在一点F,使得BF∥平面ACE.

(1)正方形ABCD边长为1,PA=1,PB=PD=
,
所以,∠PAB=∠PAD=90°,即PA⊥AB,PA⊥AD,AB∩AD=A,
根据直线和平面垂直的判定定理,
有PA⊥平面ABCD.
(2)如图,以A为坐标原点,直线AB、AD、AP分别x轴、y轴、z轴,建立空间直角坐标系.
则
=(1,1,0),
=(0,
,
),
由(1)知
为平面ACD的法向量,
=(0,0,1),
设平面ACE的法向量为
=(a,b,c),
则
令c=6,则b=-3,a=3,
=(3,-3,6),…(4分)
设二面角D-AC-E的平面角为θ,则|cosθ|=
=
,
又有图可知,θ为锐角,
故所求二面角的余弦值为
.
(3)设
=λ
(λ∈[0,1]),则
=λ(1,1,-1)=(λ,λ,-λ),
=
+
=(λ-1,λ,1-λ),
若BF∥平面ACE,则
⊥
,即
•
=0,(λ-1,λ,1-λ)•(3,-3,6)=0,
计算得λ=
所以,存在满足题意的点,即当F是棱PC的中点时,BF∥平面ACE.…(8分)
| 2 |
所以,∠PAB=∠PAD=90°,即PA⊥AB,PA⊥AD,AB∩AD=A,
根据直线和平面垂直的判定定理,
有PA⊥平面ABCD.
(2)如图,以A为坐标原点,直线AB、AD、AP分别x轴、y轴、z轴,建立空间直角坐标系.
则
| AC |
| AE |
| 2 |
| 3 |
| 1 |
| 3 |
由(1)知
| AP |
| AP |
设平面ACE的法向量为
| n |
则
|
令c=6,则b=-3,a=3,
| n |
设二面角D-AC-E的平面角为θ,则|cosθ|=
|
| ||||
|
|
| ||
| 3 |
又有图可知,θ为锐角,
故所求二面角的余弦值为
| ||
| 3 |
(3)设
| PF |
| PC |
| PF |
| BF |
| BP |
| PF |
若BF∥平面ACE,则
| BF |
| n |
| BF |
| n |
计算得λ=
| 1 |
| 2 |
所以,存在满足题意的点,即当F是棱PC的中点时,BF∥平面ACE.…(8分)


练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
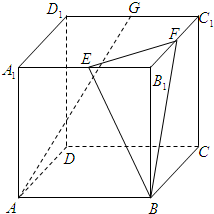
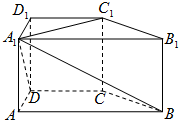
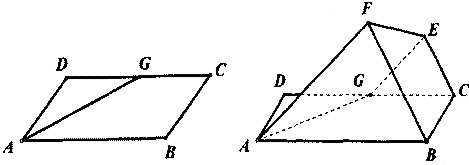

 为平行四边形,若向量
为平行四边形,若向量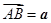 ,
,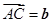 ,则向量
,则向量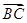 为( )
为( )