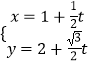题目内容
【题目】已知向量![]() ,
, ![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)把向量![]() 的坐标代入
的坐标代入![]() ,由两角和的正弦公式对解析式整理,再由题设条件
,由两角和的正弦公式对解析式整理,再由题设条件![]() ,时
,时![]() ,最后对
,最后对![]() 分类讨论,求出对应的最大值。
分类讨论,求出对应的最大值。
(2)把![]() 的值代入求出函数的周期,再由条件和正弦函数的图象求出
的值代入求出函数的周期,再由条件和正弦函数的图象求出![]() 的值,再由正弦函数的单调区间和整体思想求出增区间,再结合
的值,再由正弦函数的单调区间和整体思想求出增区间,再结合![]() 的范围求出递增区间即可。
的范围求出递增区间即可。
试题解析:(Ⅰ)由已知得, ![]()
![]()
![]() 时,
时, ![]()
当![]() 时,
时, ![]() 的最大值为
的最大值为![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() 的最大值为
的最大值为![]() ,故
,故![]() (舍去)
(舍去)
综上:函数![]() 在
在![]() 上的最大值为3时,
上的最大值为3时, ![]()
(Ⅱ)当![]() 时,
时, ![]() ,
,
由![]() 的最小正周期为
的最小正周期为![]() 可知,
可知, ![]() 的值为
的值为![]() .
.
又由![]() ,可得,
,可得,
![]() ,
,
∵![]() ,
,
∴函数![]() 在
在![]() 上的单调递减区间为
上的单调递减区间为![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目