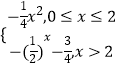题目内容
【题目】已知函数 ![]() 的值域为集合A,关于x的不等式
的值域为集合A,关于x的不等式 ![]() 的解集为B,集合
的解集为B,集合 ![]() ,集合D={x|m+1≤x<2m﹣1}(m>0)
,集合D={x|m+1≤x<2m﹣1}(m>0)
(1)若A∪B=B,求实数a的取值范围;
(2)若DC,求实数m的取值范围.
【答案】
(1)解:因为f(x)在[ ![]() ,4]上,单调递增,
,4]上,单调递增,
∵f( ![]() )=
)= ![]() =﹣2,f(4)=log44=1,
=﹣2,f(4)=log44=1,
所以,A=[﹣2 1].
又由关于x的不等式 ![]() 可得 (2)﹣3x﹣a>2x,﹣3x﹣a>x x<﹣
可得 (2)﹣3x﹣a>2x,﹣3x﹣a>x x<﹣ ![]() ,
,
所以,B=(﹣∞,﹣ ![]() ).
).
又A∪B=B,∴AB.
所以,﹣ ![]() >1,a<﹣4,即实数a的取值范围为(﹣∞,﹣4)
>1,a<﹣4,即实数a的取值范围为(﹣∞,﹣4)
(2)解:因为 ![]() ,所以有
,所以有 ![]() ,所以﹣1<x≤5,所以,C=(﹣1,5],
,所以﹣1<x≤5,所以,C=(﹣1,5],
对于集合D={x|m+1≤x<2m﹣1}(m>0),若DC,有:
①当 m+1≥2m﹣1时,即 0<m≤2时,D=,满足 DC.
②当 m+1<2m﹣1 时,即 m>2时,D≠,所以有: ![]() ,解得﹣2<m≤3,又 m>2,2<m≤3.
,解得﹣2<m≤3,又 m>2,2<m≤3.
综上:由①②可得:实m的取值范围为(0,3]
【解析】(1)利用对数函数的单调性求对数函数的值域A,解指数不等式求出B,再根据AB可得﹣ ![]() >1,由此求得实数a的取值范围.(2)解分式不等式
>1,由此求得实数a的取值范围.(2)解分式不等式 ![]() 求得C,对于集合D={x|m+1≤x<2m﹣1}(m>0),由DC,分D=和 D≠两种情况,分别求出实m的取值范围,再取并集,即得所求.
求得C,对于集合D={x|m+1≤x<2m﹣1}(m>0),由DC,分D=和 D≠两种情况,分别求出实m的取值范围,再取并集,即得所求.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目