题目内容

【题目】已知椭圆： 的上下顶点分别为，且点． 分别为椭圆的左、右焦点，且．

（Ⅰ）求椭圆的标准方程；

（Ⅱ）点是椭圆上异于， 的任意一点，过点作轴于， 为线段

的中点．直线与直线交于点， 为线段的中点， 为坐标原点．求

的大小．

【答案】（1）（2）见解析

【解析】试题分析：（1）由顶点坐标得再在中利用椭圆几何条件得．（2）利用向量数量积研究的大小．先设 ，则得 ．求出直线与直线交点，得 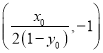．再根据向量数量积得，根据代入化简得，即得．

试题解析：解：(Ⅰ)依题意，得．又，

在中， ，所以．

所以椭圆的标准方程为．

(Ⅱ)设 ， ，则 ， ．

因为点在椭圆上，所以．即．

又 ，所以直线的方程为．

令，得 ．

又 ， 为线段的中点，所以 ．

所以， ．

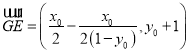因为

，

所以． ．

练习册系列答案
相关题目

【题目】已知函数（， ， ），是自然对数的底数．

（Ⅰ）当， 时，求函数的零点个数；

（Ⅱ）若，求在上的最大值．

【题目】已知椭圆： （）的左焦点与抛物线的焦点重合，直线与以原点为圆心，以椭圆的离心率为半径的圆相切．

（Ⅰ）求该椭圆的方程；

（Ⅱ）过点的直线交椭圆于， 两点，线段的中点为， 的垂直平分线与轴和轴分别交于， 两点．记的面积为， 的面积为．问：是否存在直线，使得，若存在，求直线的方程，若不存在，说明理由．

【题目】设命题p：f（x）= 在区间（1，+∞）上是减函数；命题q；x1x2是方程x2﹣ax﹣2=0的两个实根，不等式m2+5m﹣3≥|x1﹣x2|对任意实数α∈[﹣1，1]恒成立；若￢p∧q为真，试求实数m的取值范围．

【题目】已知向量， ，且函数.

（Ⅰ）当函数在上的最大值为3时，求的值；

（Ⅱ）在（Ⅰ）的条件下，若对任意的，函数， 的图像与直线有且仅有两个不同的交点，试确定的值.并求函数在上的单调递减区间.

【题目】二次函数y=ax2+bx和反比例函数 在同一坐标系中的图象大致是（ ）
A.
B.
C.
D.

【题目】对于定义域为I的函数y=f（x），如果存在区间[m，n]I，同时满足：
①f（x）在[m，n]内是单调函数；
②当定义域是[m，n]，f（x）值域也是[m，n]，则称[m，n]是函数y=f（x）的“好区间”．
（1）设g（x）=loga（ax﹣2a）+loga（ax﹣3a）（其中a＞0且a≠1），求g（x）的定义域并判断其单调性；
（2）试判断（1）中的g（x）是否存在“好区间”，并说明理由；
（3）已知函数P（x）= （t∈R，t≠0）有“好区间”[m，n]，当t变化时，求n﹣m 的最大值．

【题目】小张在淘宝网上开一家商店，他以10元每条的价格购进某品牌积压围巾2000条．定价前，小张先搜索了淘宝网上的其它网店，发现：A商店以30元每条的价格销售，平均每日销售量为10条；B商店以25元每条的价格销售，平均每日销售量为20条．假定这种围巾的销售量t（条）是售价x（元）（x∈Z+）的一次函数，且各个商店间的售价、销售量等方面不会互相影响．
（1）试写出围巾销售每日的毛利润y（元）关于售价x（元）（x∈Z+）的函数关系式（不必写出定义域），并帮助小张定价，使得每日的毛利润最高（每日的毛利润为每日卖出商品的进货价与销售价之间的差价）；
（2）考虑到这批围巾的管理、仓储等费用为200元/天（只要围巾没有售完，均须支付200元/天，管理、仓储等费用与围巾数量无关），试问小张应该如何定价，使这批围巾的总利润最高（总利润=总毛利润﹣总管理、仓储等费用）？

【题目】对于R上的可导函数f（x），若a＞b＞1且有（x﹣1）f′（x）≥0，则必有（ ）
A.f（a）+f（b）＜2f（1）
B.f（a）+f（b）≤2f（1）
C.f（a）+f（b）≥2f（1）
D.f（a）+f（b）＞2f（1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网