题目内容
【题目】下列命题正确的是( )
A.命题“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1<0
B.命题“若x=3,则x2﹣2x﹣3=0”的否命题是:若x≠3,则x2﹣2x﹣3≠0
C.“ ![]() ”是“
”是“ ![]() ”的必要而不充分条件
”的必要而不充分条件
D.命题“cosx=cosy,则x=y”的逆否命题是真命题
【答案】B
【解析】解:对于A,“x∈R,使得x2﹣1<0”的否定是:x∈R,均有x2﹣1≥0,命题A错误;
对于B,“若x=3,则x2﹣2x﹣3=0”的否命题是:若x≠3,则x2﹣2x﹣3≠0,命题B正确;
对于C, ![]() 时,
时, ![]() ,充分性成立;
,充分性成立;
![]() 时,α=kπ+
时,α=kπ+ ![]() 或α=kπ+
或α=kπ+ ![]() ,k∈Z,必要性不成立;
,k∈Z,必要性不成立;
是充分不必要条件,命题B错误;
对于D,命题“cosx=cosy,则x=y”是假命题,
则它的逆否命题也是假命题,∴命题D错误.
故选:B.
根据四种命题之间的关系,对每一个命题判断真假性即可.

练习册系列答案
相关题目
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
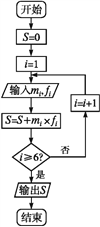
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.