题目内容
【题目】已知函数f(x)= ![]() (m,n∈R)在x=1处取得极值2.
(m,n∈R)在x=1处取得极值2.
(1)求f(x)的解析式;
(2)k为何值时,方程f(x)﹣k=0只有1个根
(3)设函数g(x)=x2﹣2ax+a,若对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),求a的取值范围.
【答案】
(1)解:因为函数f(1)= ![]() .
.
所以m=2+2n,f(x)= ![]() ,
,
又f(x)在x=1处取得极值,
f  =
= ![]() ,
,
f ![]() ,n=1,则m=4,
,n=1,则m=4,
经检验满足题意,
所以 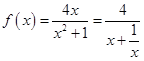 ;
;
(2)解:由f(x)﹣k=0,得k=f(x),
由(1)得f ![]() ,
,
令f′(x)=0,得x=±1.
当x变化时,f′(x),f(x)的变化情况如下表:
x | (﹣∞,﹣1) | ﹣1 | (﹣1,1) | 1 | (1,+∞) |
f'(x) | ﹣ | 0 | + | 0 | ﹣ |
f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
所以f(x)在x=﹣1处取得极小值﹣2,在x=1处取得极大值2
又 ![]() 如图
如图
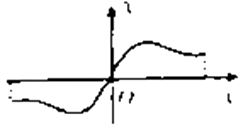
所以k=±2或0时,方程有一个根
(3)解:对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),
只需g(x2)min≤f(x1)min,
即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立
只需 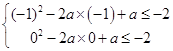 ,
,
解得a≤﹣2
a的取值范围为a≤﹣2
【解析】(1)函数f(1)= ![]() .所以m=2+2n,f(x)=
.所以m=2+2n,f(x)= ![]() ,又f(x)在x=1处取得极值,f
,又f(x)在x=1处取得极值,f ![]() ,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f
,n=1,则m=4(2)由f(x)﹣k=0,得k=f(x),由(1)得f ![]() ,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需
,令f′(x)=0,得x=±1.求出单调区间,根据图象即可求解.(3)对于任意x1∈R,总存在x2∈[﹣1,0],使得g(x2)≤f(x1),只需g(x2)min≤f(x1)min,即当x∈[﹣1,0]时,x2﹣2ax+a≤﹣2恒成立,只需 ![]() ,解得a.
,解得a.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案