题目内容
【题目】已知函数f（x）=x2﹣ax﹣aln（x﹣1）（a∈R）
（1）当a=1时，求函数f（x）的最值；
（2）求函数f（x）的单调区间．
【答案】
（1）解：函数f（x）=x2﹣ax﹣aln（x﹣1）（a∈R）的定义域是（1，+∞）
当a=1时，f（x）=x2﹣x﹣ln（x﹣1），
，
当x∈ 
时，f′（x）＜0，
所以f （x）在 为减函数．
当x∈ 
时，f′（x）＞0，
所以f （x）在 为增函数，
则当x= 
时，f（x）有极小值，也就是最小值．
所以函数f （x）的最小值为 
= 
（2）解： 
，
若a≤0时，则 
，f（x）=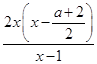 
＞0在（1，+∞）恒成立，
所以f（x）的增区间为（1，+∞）．
若a＞0，则 
，故当 
，f′（x）= ≤0，
当 
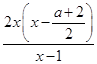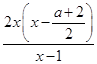时，f（x）= ≥0，
所以a＞0时f（x）的减区间为 
，f（x）的增区间为 
【解析】（1）首先求出函数的定义域，把a=1代入函数解析式后，求出函数的导函数，由导函数等于0求出函数的极值点，结合定义域可得函数在定义域内取得最值的情况，从而求出函数的最值．（2）把原函数求导后，对参数a进行分类，根据a的不同取值得到导函数在不同区间内的符号，从而得到原函数的单调区间．
【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼，随机抽取50条作为样本进行统计，按海鱼重量（克）得到如图的频率分布直方图： 
（Ⅰ）若经销商购进这批海鱼100千克，试估计这批海鱼有多少条（同一组中的数据用该区间的中点值作代表）；
（Ⅱ）根据市场行情，该海鱼按重量可分为三个等级，如下表：
等级 | 一等品 | 二等品 | 三等品 |
重量（g） | [165，185] | [155，165） | [145，155） |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据，视频率为概率．现从这批海鱼中随机抽取3条，记抽到二等品的条数为X，求x的分布列和数学期望．
