Ő‚ńŅńŕ»›
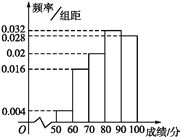
°ĺŐ‚ńŅ°Ņő“–£∂‘łŖ∂Ģ600√Ż—ß…ķĹÝ––Ńň“Ľīő÷™ ∂≤‚ ‘,≤Ęī”÷–≥ť»°Ńň≤Ņ∑÷—ß…ķĶń≥…ľ®(¬ķ∑÷100∑÷)◊ųő™—ýĪĺ,Ľś÷∆ŃňŌ¬√ś…–őīÕÍ≥…Ķń∆Ķ¬ ∑÷≤ľĪŪļÕ∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ.

(1)ŐÓ–ī∆Ķ¬ ∑÷≤ľĪŪ÷–ĶńŅ’łŮ,≤Ļ»ę∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ,≤ĘĪÍ≥Ų√ŅłŲ–°ĺō–ő∂‘”¶Ķń◊›÷Š żĺ›;
(2)«Žń„Ļņň„ł√ńÍľ∂—ß…ķ≥…ľ®Ķń÷–őĽ ż;
(3)»ÁĻŻ”√∑÷≤„≥ť—ýĶń∑Ĺ∑®ī”—ýĪĺ∑÷ ż‘ŕ[60,70)ļÕ[80,90)Ķń»ň÷–Ļ≤≥ť»°6»ň,‘Ŕī”6»ň÷–—°2»ň,«ů2»ň∑÷ ż∂ľ‘ŕ[80,90)ĶńłŇ¬ .

°ĺīūįł°Ņ(1)ľŻĹ‚őŲ£Ľ(2)83.125.(3)![]() .
.
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ (1)Ō»ŐÓ–īÕÍ’Ż∆Ķ¬ ∑÷≤ľĪŪ,”…īňń‹≤Ļ»ę∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ.
(2)…Ť÷–őĽ żő™x,ņŻ”√∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľŃ–≥Ų∑Ĺ≥Ő,łÝ«ů≥Ų÷–őĽ ż.
(3)”…Ő‚“‚÷™—ýĪĺ∑÷ ż‘ŕ[60,70)”–8»ň,—ýĪĺ∑÷ ż‘ŕ[80,90)”–16»ň,”√∑÷≤„≥ť—ýĶń∑Ĺ∑®ī”—ýĪĺ∑÷ ż‘ŕ[60,70)ļÕ[80,90)Ķń»ň÷–Ļ≤≥ť»°6»ň,‘Ú≥ť»°Ķń∑÷ ż‘ŕ[60,70)ļÕ[80,90)Ķń»ň ż∑÷Īūő™2»ňļÕ4»ň.ľ«∑÷ ż‘ŕ[60,70)ő™a1,a2£¨[80,90)Ķńő™b1,b2,b3,b4.”…īňņŻ”√Ń–ĺŔ∑®ń‹«ů≥Ų2»ň∑÷ ż∂ľ‘ŕ[80,90)ĶńłŇ¬ .
‘Ő‚Ĺ‚őŲ£ļ(1)ŐÓ–ī∆Ķ¬ ∑÷≤ľĪŪ÷–ĶńŅ’łŮ,»ÁŌ¬ĪŪ:
∑÷°°◊ť | ∆Ķ°° ż | ∆Ķ°°¬ |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | 0.2 |
[80,90) | 16 | 0.32 |
[90,100] | 14 | 0.28 |
ļŌ°°ľ∆ | 50 | 1.00 |
»ę∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ,»ÁŌ¬Õľ:
(2)…Ť÷–őĽ żő™x,“ņŐ‚“‚Ķ√0.04+0.16+0.2+0.032°Ń(x-80)=0.5,
Ĺ‚Ķ√x=83.125,ňý“‘÷–őĽ ż‘ľő™83.125.
(3)”…Ő‚“‚÷™—ýĪĺ∑÷ ż‘ŕ[60,70)”–8»ň,—ýĪĺ∑÷ ż‘ŕ[80,90)”–16»ň,
”√∑÷≤„≥ť—ýĶń∑Ĺ∑®ī”—ýĪĺ∑÷ ż‘ŕ[60,70)ļÕ[80,90)Ķń»ň÷–Ļ≤≥ť»°6»ň,
‘Ú≥ť»°Ķń∑÷ ż‘ŕ[60,70)ļÕ[80,90)Ķń»ň ż∑÷Īūő™2»ňļÕ4»ň.
ľ«∑÷ ż‘ŕ[60,70)Ķńő™a1,a2,‘ŕ[80,90)Ķńő™b1,b2,b3,b4.
ī”“—≥ť»°Ķń6»ň÷–»ő—°ŃĹ»ňĶńňý”–Ņ…ń‹ĹŠĻŻ”–15÷÷,∑÷Īūő™{a1,a2},{a1,b1},{a1,b2},{a1,b3},{a1,b4},{a2,b1},{a2,b2},{a2,b3},{a2,b4},{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4},
…Ť°į2»ň∑÷ ż∂ľ‘ŕ[80,90)°Īő™ ¬ľĢA,
‘Ú ¬ľĢAįŁņ®{b1,b2},{b1,b3},{b1,b4},{b2,b3},{b2,b4},{b3,b4}Ļ≤6,ňý“‘P(A)=![]() .
.


