题目内容
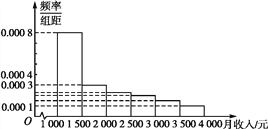
【题目】已知函数f（x）=x3+bx2+cx+d的图象如图，则函数 
的单调递减区间是（ ） 
A.（﹣∞，﹣2）
B.（﹣∞，1）
C.（﹣2，4）
D.（1，+∞）
【答案】A
【解析】解：∵f（x）=x3+bx2+cx+d，∴f′（x）=3x2+2bx+c，∴ 
，
由图可知f′（﹣2）=f（3）=0，∴解得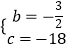 
，
∵y=log2（x2+ 
bx+ 
）═log2（x2﹣x﹣6），令g（x）=x2﹣x﹣6=（x+2）（x﹣3）．
本题即求当g（x）＞0时，g（x）的减区间．
由二次函数的性质可得当g（x）＞0时，g（x）的减区间为（﹣∞，﹣2），
故选：A．
求出原函数的导函数，由图象得到f′（﹣2）=f（3）=0，联立求得b，c的值，由g（x）＞0求得x的范围，再由二次函数的性质求出函数g（x）的减区间，则函数y的单调递减区间可求．
练习册系列答案
相关题目
