Question

【题目】数列{an}满足an+1= （n∈N*），且a1=0， （Ⅰ）计算a2、a3、a4 ， 并推测an的表达式；
（Ⅱ）请用数学归纳法证明你在（Ⅰ）中的猜想．

Answer 1

【答案】解：（ I） a2= ； a3= ； a4= = ，

由此猜想an= （n∈N*）；

（ II）证明：（数学归纳法）

①当n=1时，a1=0，结论成立，

②假设n=k（k≥1，且k∈N*）时结论成立，

即ak= ，

当n=k+1时，ak+1= ，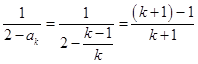

∴当n=k+1时结论成立，

由①②知：对于任意的n∈N*，a 恒成立

【解析】本题先根据题目中递推关系式，由a1=0，求出a2、a3、a4，并推测an的表达式，然后用数学归纳法加以证明，得到本题结论．
【考点精析】本题主要考查了归纳推理的相关知识点，需要掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理才能正确解答此题．