Question

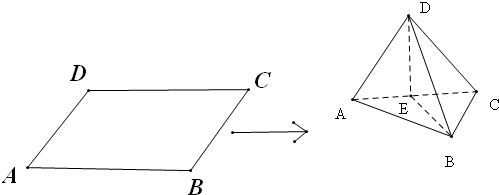
将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则AD与平面ABC所成之角为______．

Answer 1

如图，由题意知DE=BE=

2

2

a，BD=a
由勾股定理可得∠BED=90°，故△BDE面积是

1

4

a²
又正方形的对角线互相垂直，且翻折后，AC与DE，BE仍然垂直，
故AE，CE分别是以面BDE为底的两个三角形的高
故三棱锥D-ABC的体积为

1

3

×

2

a×

1

4

a²=

2

12

a3，
设点D到平面ABC的距离为h，则
∵三棱锥D-ABC的体积为

1

3

S△ABCh=

1

6

a2h，
∴

2

12

a3═

1

6

a2h，
∴h=

2

2

a，
设AD与平面ABC所成角为α，则sinα=

2 2 a

a

=

2

2

，
∴α=45°．
故答案为：45°．