题目内容
在矩形ABCD中,AB=3,AD=4,PA⊥平面ABCD,PA=
,那么二面角A-BD-P的大为( )
| 4 |
| 5 |
| 3 |
| A.30° | B.45° | C.60° | D.75° |
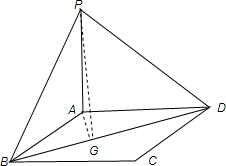
在平面ABCD,作AG⊥BD于G
∵PA⊥平面ABCD,则PA⊥BD,PA⊥AG,又AG⊥BD
∴BD⊥平面PAG,则BD⊥PG
所以∠PGA等于所求的二面角A-BD-P.
因为图形ABCD是矩形,AD=4,AB=3,AG垂直BD,
所以 AD:AG=BD:AB 即4:AG=5:3,则AG=
在直角三角形PGA中,∠A=90°,PA=
,AG=
则
tan∠PGA=
÷
=
∴∠PGA=30°
故选A
∵PA⊥平面ABCD,则PA⊥BD,PA⊥AG,又AG⊥BD
∴BD⊥平面PAG,则BD⊥PG
所以∠PGA等于所求的二面角A-BD-P.
因为图形ABCD是矩形,AD=4,AB=3,AG垂直BD,
所以 AD:AG=BD:AB 即4:AG=5:3,则AG=
| 12 |
| 5 |
在直角三角形PGA中,∠A=90°,PA=
| 4 |
| 5 |
| 3 |
| 12 |
| 5 |
tan∠PGA=
| 4 |
| 5 |
| 3 |
| 12 |
| 5 |
| ||
| 3 |
∴∠PGA=30°
故选A


练习册系列答案
相关题目



