题目内容
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
【答案】(1)![]() ;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
;(2)①见证明;②当n=2,m=4时,λ=-2,当n=2,m=3时,λ=-1.
【解析】
(1)先求解等差数列![]() 的通项公式,再根据
的通项公式,再根据![]() 求解
求解![]() 的通项公式;(2)①采用错位相减法先求
的通项公式;(2)①采用错位相减法先求![]() ,再根据
,再根据 ,证明
,证明![]() 为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即
为等比数列;②将所给的等式变形,然后得到对应的等量关系,接着分析此等量关系(借助数列的单调性)在什么时候满足即![]() 取什么值时能满足要求.
取什么值时能满足要求.
(1)因为![]() ,所以
,所以![]()
所以![]()
即![]()
当![]() 时,
时,![]()
∴![]()
当n=1时,![]() ,符合上述通项,所以
,符合上述通项,所以![]()
(2)①因为![]() ,所以
,所以![]()
所以![]()
则![]()
两式相减,可整理得![]()
∴![]() ,
,![]() ,且
,且![]()
所以数列![]() 是以4为首项,2为公比的等比数列.
是以4为首项,2为公比的等比数列.
②由①可知,![]() ,且由(1)知
,且由(1)知![]() ,代入
,代入![]()
可得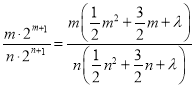
整理得![]()
即:![]() ,设
,设![]() ,则
,则![]()
则![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]()
因为![]() ,且
,且![]()
所以![]()
所以![]() 或
或![]() ,即n=2,m=4或3
,即n=2,m=4或3
当n=2,m=4时,λ=-2,
当n=2,m=3时,λ=-1.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目