题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,设
时,设![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)详见解析(2)证明见解析。
【解析】
(1)利用导函数分子的判别式分情况讨论,即可,注意参数![]() 时,函数图像开口也会发生相应的变化。(2)利用对数平均不等式,证明即可。
时,函数图像开口也会发生相应的变化。(2)利用对数平均不等式,证明即可。
解:(1)![]() ,
,![]() ,
,
对于一元二次方程![]() ,
,![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() 无解或一个解,
无解或一个解,
有![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() 时,即
时,即![]() 时,
时,![]() 有两个解,
有两个解,
其解为![]() , 当
, 当![]() 时,
时,![]() ,故在
,故在![]() 及
及![]() 时,
时,![]() ;且
;且![]() 时,
时,![]() ,即
,即![]() 在
在![]() 及
及![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 时,一个实根小于0,一个实根大于0,所以在
时,一个实根小于0,一个实根大于0,所以在![]() 时,
时,![]() ,在
,在![]() ,
,![]() ,即
,即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
综上所述:即![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,即
时,即![]() 在
在![]() 及
及![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
(2)当![]() 时,
时,![]() ,
,![]() ,又因为
,又因为![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,则
,则![]() ,
,![]() 是方程
是方程![]() 的两实数根,
的两实数根,![]() 设
设![]() 。
。
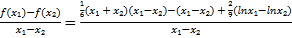
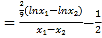
又因为![]() ,故要证
,故要证![]() ,
,
只需证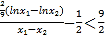 ,
,
只需证![]() ,
,
只需证![]() ,
,
下面证明不等式![]() ,不妨设
,不妨设![]() ,要证
,要证![]() ,即证
,即证![]() ,即证
,即证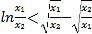 ,令
,令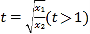 ,设
,设![]() ,则
,则![]() ,所以,函数
,所以,函数![]() 在
在![]() 上递减,而
上递减,而![]() ,因此当
,因此当![]() 时,
时,![]() 恒成立,即
恒成立,即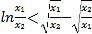 成立,即
成立,即![]() 成立,
成立,
所以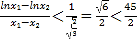 ,得证。
,得证。

 科学实验活动册系列答案
科学实验活动册系列答案【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
【题目】火箭少女101的新曲《卡路里》受到了广大听众的追捧,歌词积极向上的体现了人们对于健康以及完美身材的渴望.据有关数据显示,成年男子的体脂率在14%-25%之间.几年前小王重度肥胖,在专业健身训练后,身材不仅恢复正常,且走上美体路线.通过整理得到如下数据及散点图.
健身年数 | 1 | 2 | 3 | 4 | 5 | 6 |
体脂率 | 32 | 20 | 12 | 8 | 6.4 | 4.4 |
| 3.4 | 3 | 2.5 | 2.1 | 1.9 | 1.5 |
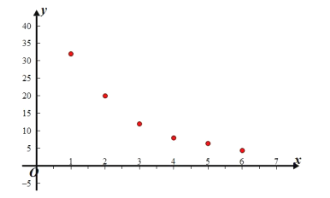
(1)根据散点图判断,![]() 与
与![]() 哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
哪一个模型更适宜作为体脂率关于健身年数的回归方程模型(给出选择即可)
(2)根据(1)的判断结果与题目中所给数据,建立![]() 与
与![]() 的回归方程.(保留一位小数)
的回归方程.(保留一位小数)
(3)再坚持3年,体脂率可达到多少.
参考公式: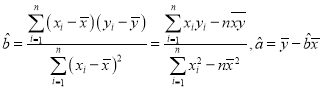
参考数据:![]()