题目内容
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
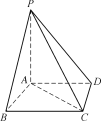
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)先求得平面PBC的一个法向量,易知平面PAD的一个法向量,再利用面面角的向量方法求解.
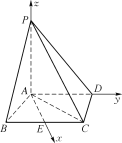
(1) 设BC的中点为E,由AB=AC,可知AE⊥BC,
故分别以AE,AD,AP所在的直线为x,y,z轴建立空间直角坐标系
则A(0,0,0),P(0,0,4),D(0,3,0),B(![]() ,-2,0),C(
,-2,0),C(![]() ,2,0).
,2,0).
设θ为两直线所成的角,
由![]() =(
=(![]() ,-2,-4),
,-2,-4),![]() =(-
=(-![]() ,1,0),
,1,0),
得cosθ=![]() =
=![]() .
.
(2) 设![]() =(x,y,z)为平面PBC的法向量,
=(x,y,z)为平面PBC的法向量,
![]() =(
=(![]() ,-2,-4),
,-2,-4),![]() =(
=(![]() ,2,-4),
,2,-4),
![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,
=0,
即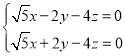
取平面PBC的一个法向量![]() =(4,0,
=(4,0,![]() ),
),
平面PAD的一个法向量为![]() =(1,0,0).
=(1,0,0).
设α为两个平面所成的锐二面角的平面角,则cosα=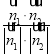 =
=![]() .
.
所以平面PAD与平面PBC所成锐二面角的余弦值为![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目