题目内容
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求C的方程;
(2)若直线l与C有且只有一个公共点,l与圆x2+y2=6交于A,B两点,直线OA,OB的斜率分别记为k1,k2.试判断k1k2是否为定值,若是,求出该定值;否则,请说明理由.
【答案】(1)![]() ;(2)k1k2为定值
;(2)k1k2为定值![]() .
.
【解析】
(1)由题意可得关于a,b,c的方程组,求解a,b,c的值,即可得到椭圆的方程;
(2)①当过点P的直线斜率不存在时,直线的方程为x=±2,求得![]() ,②当过P的直线斜率存在时,设其方程为y=kx+m,联立直线方程与椭圆方程,由判别式等于0可得m2=4k2+2,联立直线方程与椭圆方程,利用根与系数的关系结合斜率公式可得
,②当过P的直线斜率存在时,设其方程为y=kx+m,联立直线方程与椭圆方程,由判别式等于0可得m2=4k2+2,联立直线方程与椭圆方程,利用根与系数的关系结合斜率公式可得![]() 为定值
为定值![]() .
.
(1)由题意,得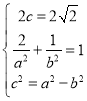 ,
,
解得![]() .
.
∴椭圆C的方程为![]() .
.
(2)k1k2为定值![]()
理由如下:
①当过点P的直线斜率不存在时,直线的方程为x=±2;
当x=2时,![]() ,则
,则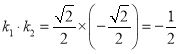 ,
,
当![]() 时,
时,![]() ,则
,则![]() .
.
②当过P的直线斜率存在时,设其方程为![]() ,
,
联立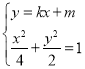 ,得
,得![]()
由题意![]() ,得
,得![]() ,
,
联立![]() ,得
,得![]()
则![]()
所以![]()
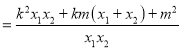
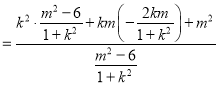
![]()
![]()
综上,![]() 为定值
为定值![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目