题目内容

11．在等差数列{an}中，a10＜0，a11＞0，且a11＞|a10|，Sn为数列{an}的前n项和，则使Sn＞0的n的最小值为（　　）
A．10B．11C．20D．21

分析 由题意可得：由等差数列的性质可得：S20=$\frac{20（{a}_{10}+{a}_{11}）}{2}$＞0，S19=19•a10＜0，所以使Sn＞0的n的最小值为20．

解答 解：由题意可得：因为a10＜0，a11＞0，且a11＞|a10|，
所以由等差数列的性质可得：S20=$\frac{20（{a}_{10}+{a}_{11}）}{2}$＞0，S19=19•a10＜0，
所以使Sn＞0的n的最小值为20．
故选：C．

点评 本题主要考查学生灵活运用等差数列的性质化简求值，掌握等差数列的前n项和公式．

练习册系列答案
相关题目
8．解方程：$\frac{a}{\sqrt{4+{a}^{2}}}$=$\frac{\sqrt{3}}{2}$．
2．已知动点P（x，y）及两定点A（-3，0）和B（3，0），若$\frac{|PA|}{|PB|}$=2，（|PA|、|PB|分别表示点P与点A、B的距离）
（1）求动点P的轨迹Γ方程．
（2）动点Q在直线y-x-1=0上，且QM、QN是轨迹Γ的两条切线，M、N是切点，C是轨迹Γ中心，求四边形OMCN面积的最小值及此时直线MN的方程．
19．设f′（x）是f（x）的导函数，f″（x）是f′（x）的导函数，若函数f（x）在区间I上恒有f″（x）≥0，则称f（x）是区间I上的凸函数，则下列函数在[-1，1]上是凸函数的是（　　）
A．f（x）=sinxB．f（x）=-cosxC．f（x）=x3-xD．f（x）=-ex
6．已知椭圆C：$\frac{{x}^{2}}{m}$+y2=1，现有命题P：“若m=4，则椭圆C的离心率为$\frac{\sqrt{3}}{2}$”，记命题P和它的逆命题，否命题，逆否命题四种形式的命题中正确的命题的个数为f（P），则f（P）=2．
16．已知函数f（x）=lnx-ax，a∈R．
（1）若a=1，求函数f（x）的单调区间；
（2）求证：对任意给定的正数m，总存在实数a，使函数f（x）在区间（m，+∞）上不单调；
（3）试探究：是否存在实数x1、x2（x2＞x1＞0），使当x∈[x1，x2]时，函数f（x）的值域为[kx1-1，kx2-1]（k∈R）？若存在，试确定实数k的取值范围；若不存在，请说明理由．
3．双曲线$\frac{y^2}{12}-\frac{x^2}{4}=1$的顶点到渐近线的距离为$\sqrt{3}$．
20．海上某货轮在A处看灯塔B在货轮的北偏东75°，距离为12$\sqrt{6}$海里；在A处看灯塔C在货轮的北偏西30°，距离为8$\sqrt{3}$海里；货轮向正北由A处行驶到D处时看灯塔B在货轮的北偏东120°．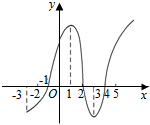
（1）请在方框内用铅笔与直尺画出图形，并标明三个角度的位置和大小；
（2）A处与D处之间的距离；
（3）灯塔C与D处之间的距离（用近似值表示，四舍五入，取整数）．
1．如图所示是y=f（x）的导数图象，则正确的判断是（　　）
①f（x）在（-3，1）上是增函数；②x=-1是f（x）的极小值点；
③f（x）在（2，4）上是减函数，在（-1，2）上是增函数；④x=2是f（x）的极小值点．
A．①②③B．②③C．③④D．①③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网