题目内容
2.已知动点P(x,y)及两定点A(-3,0)和B(3,0),若$\frac{|PA|}{|PB|}$=2,(|PA|、|PB|分别表示点P与点A、B的距离)(1)求动点P的轨迹Γ方程.
(2)动点Q在直线y-x-1=0上,且QM、QN是轨迹Γ的两条切线,M、N是切点,C是轨迹Γ中心,求四边形OMCN面积的最小值及此时直线MN的方程.
分析 (1)利用已知条件直接列出方程,即可求动点P的轨迹Γ方程.
(2)由(1)知轨迹Γ是以C(5,0)为圆心,半径为4的圆,可得|QM|=|QN|,表示出四边形面积S,然后求出Smin=4$\sqrt{2}$.线段CQ为直径的圆的方程,以及直线MN的方程.
解答 解:(1)由|PA|=$\sqrt{{(x+3)}^{2}+{y}^{2}}$,$\left|PB\right|=\sqrt{{(x-3)}^{2}+{y}^{2}}$,代入$\frac{|PA|}{|PB|}$=2,
经化简得轨迹Γ方程为(x-5)2+y2=16.
(2)由(1)知轨迹Γ是以C(5,0)为圆心,半径为4的圆,|QM|=|QN|,
易知四边形面积S=$\frac{1}{2}$(|QM|+|QN|)×4=4|QM|,故|QM|最小时,四边形QMNC面积最小.
|QM|=$\sqrt{2}$
故有Smin=4$\sqrt{2}$.
此时CQ直线:x+y=5 由$\left\{\begin{array}{l}x+y=5\\ y-x=1\end{array}\right.$ 得到Q(2,3),
以线段CQ为直径的圆的方程为:x2-7x+y2-3y+10=0.
两圆方程相减得到直线MN的方程为:3y-2x-1=0.
点评 本题考查直线方程的综合应用,在方程以及圆的方程的求法,考查计算能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
7.下列选项中,说法正确的是( )
| A. | 若命题“p∨q”为真命题,则命题p和命题q均为真命题 | |
| B. | am2<bm2是a<b的必要不充分条件 | |
| C. | x=2kπ+$\frac{π}{4}$(k∈Z)是(-sinx)′=(cosx)′的充要条件 | |
| D. | 命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底,则{$\overrightarrow{a}$,$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题 |
12.环卫工人准备在路的一侧依次栽种7棵树,现只有梧桐树和柳树可供选择,则相邻2棵树不同为柳树的栽种方法有( )
| A. | 21种 | B. | 33种 | C. | 34种 | D. | 40种 |
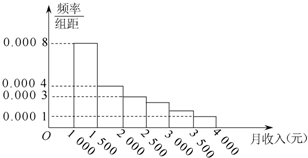 如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答:
如图是某市有关部门根据该市干部的月收入情况,作抽样调查后画出的样本频率分布直方图.已知图中第一组的频数为4000,请根据该图提供的信息 (图中每组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),回答: