题目内容
已知双曲线 -y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
 -y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程. +y2=1,x≠0
+y2=1,x≠0由题设知|x1|>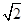 ,A1(-
,A1(-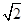 ,0),A2(
,0),A2(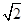 ,0),则有直线A1P的方程为y=
,0),则有直线A1P的方程为y=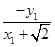 (x+
(x+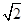 ) ①,
) ①,
直线A2Q的方程为y= (x-
(x-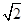 ) ②.
) ②.
联立①②,解得交点坐标为 ,即
,即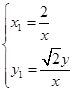 ③,则x≠0,|x|<
③,则x≠0,|x|<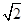 .
.
而点P(x1,y1)在双曲线 -y2=1上,所以
-y2=1上,所以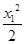 -
-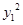 =1.
=1.
将③代入上式,整理得所求轨迹E的方程为 +y2=1,x≠0.
+y2=1,x≠0.
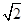 ,A1(-
,A1(-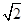 ,0),A2(
,0),A2(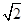 ,0),则有直线A1P的方程为y=
,0),则有直线A1P的方程为y=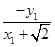 (x+
(x+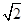 ) ①,
) ①,直线A2Q的方程为y=
 (x-
(x-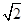 ) ②.
) ②.联立①②,解得交点坐标为
 ,即
,即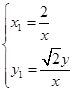 ③,则x≠0,|x|<
③,则x≠0,|x|<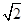 .
.而点P(x1,y1)在双曲线
 -y2=1上,所以
-y2=1上,所以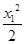 -
-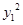 =1.
=1.将③代入上式,整理得所求轨迹E的方程为
 +y2=1,x≠0.
+y2=1,x≠0.
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 中,已知中心在坐标原点的双曲线
中,已知中心在坐标原点的双曲线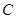 经过点
经过点 ,且它的右焦点
,且它的右焦点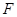 与抛物线
与抛物线 的焦点相同,则该双曲线的标准方程为 .
的焦点相同,则该双曲线的标准方程为 .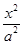 -
-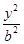 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )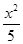 -
-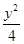 =1
=1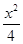 -
-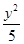 =1
=1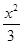 -
-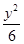 =1
=1 -
-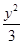 =1
=1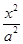 -y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )
-y2=1交于A、B两点,点F是抛物线的焦点,若△FAB为直角三角形,则该双曲线的离心率为( )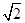 B.
B.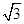 C.2 D.
C.2 D.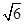
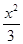 -y2=1的左,右焦点分别为F1,F2,点P在双曲线上,且满足|PF1|+|PF2|=2
-y2=1的左,右焦点分别为F1,F2,点P在双曲线上,且满足|PF1|+|PF2|=2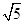 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( )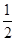
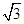
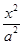 -
- =1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )
=1(a>0,b>0)的左,右焦点,若在双曲线右支上存在一点P,满足|PF2|=|F1F2|,且点F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的离心率e为( )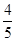
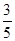
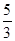
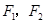 分别为双曲线
分别为双曲线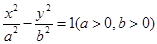 的左、右焦点,双曲线上存在一点
的左、右焦点,双曲线上存在一点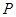 使得
使得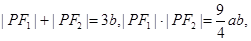 则该双曲线的离心率为
则该双曲线的离心率为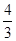
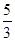
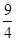
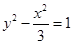 的上焦点为圆心,与该双曲线的渐近线相切的圆的方程为 .
的上焦点为圆心,与该双曲线的渐近线相切的圆的方程为 .