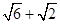题目内容
已知双曲线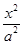 -
-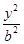 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
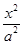 -
-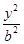 =1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )
=1(a>0,b>0)的两条渐近线均和圆C:x2+y2-6x+5=0相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程为( )A.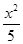 - -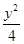 =1 =1 | B.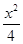 - -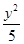 =1 =1 |
C.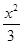 - -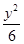 =1 =1 | D. - -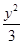 =1 =1 |
A
由x2+y2-6x+5=0知圆心C(3,0),半径r=2.
又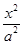 -
-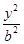 =1的渐近线为bx±ay=0,且与圆C相切.
=1的渐近线为bx±ay=0,且与圆C相切.
由直线与圆相切,得 =2,
=2,
即5b2=4a2,①
因为双曲线右焦点为圆C的圆心,所以c=3,从而9=a2+b2,②
由①②联立,得a2=5,b2=4,
故所求双曲线方程为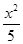 -
-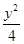 =1,选A.
=1,选A.
又
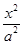 -
-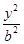 =1的渐近线为bx±ay=0,且与圆C相切.
=1的渐近线为bx±ay=0,且与圆C相切.由直线与圆相切,得
 =2,
=2,即5b2=4a2,①
因为双曲线右焦点为圆C的圆心,所以c=3,从而9=a2+b2,②
由①②联立,得a2=5,b2=4,
故所求双曲线方程为
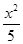 -
-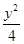 =1,选A.
=1,选A.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
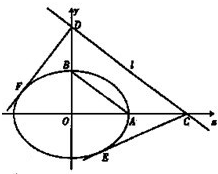
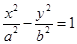 (a>b>0)的一个焦点为
(a>b>0)的一个焦点为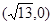 ,离心率为
,离心率为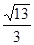 .
.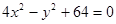 上的一点
上的一点 到一个焦点的距离等于1,那么点
到一个焦点的距离等于1,那么点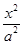 -
-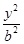 =1(a·b≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且
=1(a·b≠0,且a≠b)与直线x+y-1=0相交于P,Q两点,且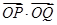 =0(O为原点),则
=0(O为原点),则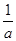 -
-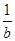 的值为________.
的值为________. -y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.
-y2=1的左、右顶点分别为A1,A2,点P(x1,y1),Q(x1,-y1)是双曲线上不同的两个动点.求直线A1P与A2Q交点的轨迹E的方程.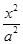 -
-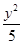 =1的右焦点为(3,0),则该双曲线的离心率等于( )
=1的右焦点为(3,0),则该双曲线的离心率等于( )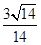
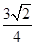
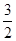
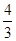
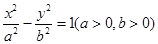 的左、右焦点,若双曲线右支上存在一点M,使
的左、右焦点,若双曲线右支上存在一点M,使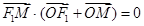 ,O为坐标原点,且
,O为坐标原点,且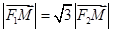 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )