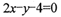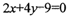题目内容
(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知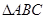 的三个顶点在抛物线
的三个顶点在抛物线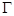 :
: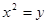 上运动,
上运动,
(1). 求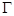 的焦点坐标;
的焦点坐标;
(2). 若点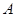 在坐标原点, 且
在坐标原点, 且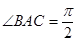 ,点
,点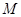 在
在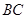 上,且
上,且 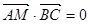 ,
,
求点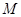 的轨迹方程;
的轨迹方程;
(3). 试研究: 是否存在一条边所在直线的斜率为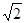 的正三角形
的正三角形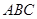 ,若存在,求出这个正三角形
,若存在,求出这个正三角形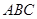 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.
已知
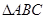 的三个顶点在抛物线
的三个顶点在抛物线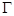 :
: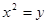 上运动,
上运动,(1). 求
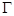 的焦点坐标;
的焦点坐标;(2). 若点
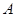 在坐标原点, 且
在坐标原点, 且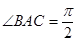 ,点
,点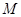 在
在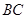 上,且
上,且 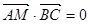 ,
,求点
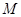 的轨迹方程;
的轨迹方程;(3). 试研究: 是否存在一条边所在直线的斜率为
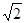 的正三角形
的正三角形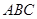 ,若存在,求出这个正三角形
,若存在,求出这个正三角形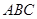 的边长,若不存在,说明理由.
的边长,若不存在,说明理由.(1) 【解】. 由
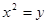 得
得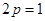 所以,焦点坐标为
所以,焦点坐标为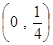 ……3分
……3分(2) 【解1】设点
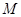 的坐标为
的坐标为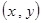 ,
,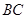 边所在的方程为
边所在的方程为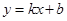 (
(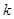 显然存在的),与抛物线
显然存在的),与抛物线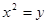 交于
交于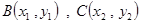
则
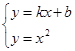 得
得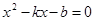 ,
,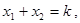
 ……5分
……5分又点
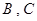 在抛物线
在抛物线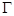 上,故有
上,故有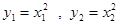 ,
, 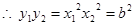
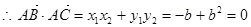
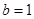 或
或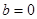 (舍)
(舍)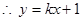 -------① ……7分
-------① ……7分又
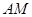 的斜率为
的斜率为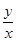 ,则有
,则有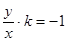 ,既
,既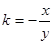 代入①
代入①故
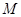 点轨迹为
点轨迹为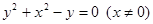 (注:没写
(注:没写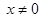 扣1分) ……9分
扣1分) ……9分另解:由上式①过定点
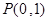 ,
,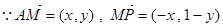
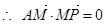 ,
, 所以,
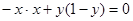 , 既
, 既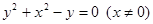
【解2】设点
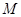 的坐标为
的坐标为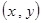 ,
,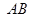 方程为
方程为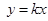 ,由
,由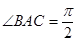 得
得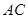 方程为
方程为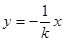 ,则
,则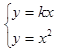 得
得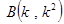 , 同理可得
, 同理可得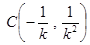
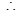
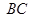 方程为
方程为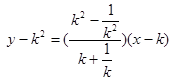 恒过定点
恒过定点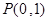 ,
,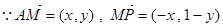
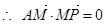 ,
, 所以,
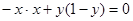 , 既
, 既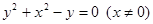
(注:没写
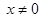 扣1分)
扣1分)(其他解法,可根据【解1】的评分标准给分)
(3) 【解1】
若存在
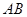 边所在直线的斜率为
边所在直线的斜率为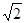 的正三角形
的正三角形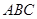 ,设
,设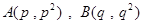 ,
,(其中不妨设
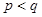 ), 则
), 则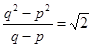 ,
, 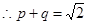 ------① ……11分
------① ……11分令
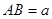 ,则
,则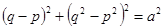 ,即
,即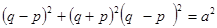
将①代入得,
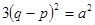 ,
, 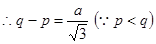 -----------------② ……13分
-----------------② ……13分线段
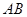 的中点为
的中点为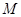 ,由①, ②得
,由①, ②得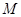 的横坐标为
的横坐标为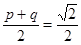 ,
,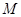 的纵坐标为
的纵坐标为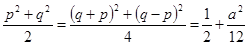 ……15分
……15分又设
 由
由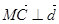 得
得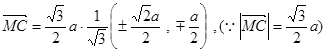
 点
点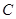 在抛物线
在抛物线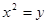 上,则
上,则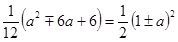 ,即
,即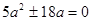 ,
,又因为
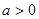 ,
, 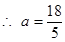 ……18分
……18分设
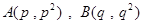 ,
,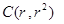
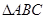 的三边所在直线
的三边所在直线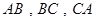 的斜率分别是
的斜率分别是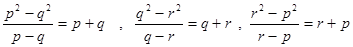 ------① ……12分
------① ……12分若
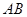 边所在直线的斜率为
边所在直线的斜率为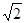 ,
,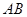 边所在直线和
边所在直线和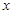 轴的正方向所成角为
轴的正方向所成角为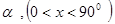 ,则
,则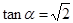 ,
,所以
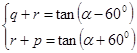 ……14分
……14分即
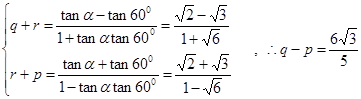 -----②
-----② 又
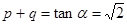 --------------③ ……16分
--------------③ ……16分所以,
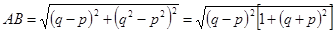
将②, ③代入上式得边长
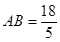 ……18分
……18分(其他解法,可根据【解1】的评分标准给分)
略

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
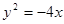 的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.
的焦点为F,其准线与x轴交于点M,过点M作斜率为k的直线l交抛物线于A、B两点,.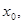 O),求证:
O),求证: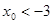
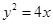 上,则该点到点
上,则该点到点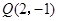 的距离与到抛物线焦点距离之和取得最小值时的坐标为( )
的距离与到抛物线焦点距离之和取得最小值时的坐标为( )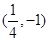
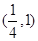
 有相同的焦点F,点A是两曲线的交点,且AF
有相同的焦点F,点A是两曲线的交点,且AF 轴,则双曲线的离心率为 .
轴,则双曲线的离心率为 .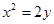 上距离点A
上距离点A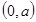 的最近点恰好是抛物线的顶点,则
的最近点恰好是抛物线的顶点,则 的取值范围是( )
的取值范围是( )
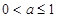
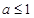


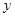 =4
=4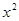 的焦点坐标是( )
的焦点坐标是( )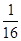 )
)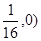
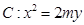
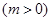 和直线
和直线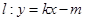 没有公共点(其中
没有公共点(其中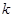 、
、 为常数),动点
为常数),动点 是直线
是直线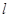 上的任意一点,过
上的任意一点,过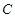 的两条切线,切点分别为
的两条切线,切点分别为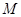 、
、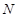 ,且直线
,且直线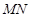 恒过点
恒过点 .
.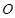 点为原点,连结
点为原点,连结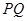 交抛物线
交抛物线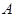 、
、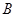 两点,
两点,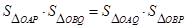 .
.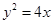 的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使
的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使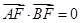 ,则直线AB的斜率
,则直线AB的斜率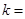 ( )
( )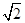 B
B 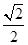 C
C 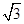 D
D 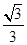
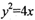 交于A,B两点;线段AB中点为
交于A,B两点;线段AB中点为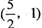 ,则直线l的方程为
,则直线l的方程为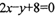
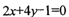 、
、