题目内容
(本小题满分14分)
已知抛物线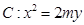
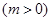 和直线
和直线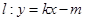 没有公共点(其中
没有公共点(其中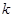 、
、 为常数),动点
为常数),动点 是直线
是直线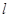 上的任意一点,过
上的任意一点,过 点引抛物线
点引抛物线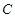 的两条切线,切点分别为
的两条切线,切点分别为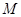 、
、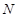 ,且直线
,且直线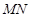 恒过点
恒过点 .
.
(1)求抛物线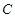 的方程;
的方程;
(2)已知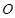 点为原点,连结
点为原点,连结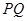 交抛物线
交抛物线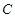 于
于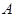 、
、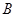 两点,
两点,
证明: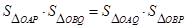 .
.
已知抛物线
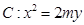
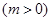 和直线
和直线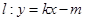 没有公共点(其中
没有公共点(其中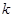 、
、 为常数),动点
为常数),动点 是直线
是直线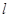 上的任意一点,过
上的任意一点,过 点引抛物线
点引抛物线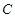 的两条切线,切点分别为
的两条切线,切点分别为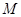 、
、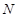 ,且直线
,且直线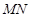 恒过点
恒过点 .
.(1)求抛物线
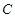 的方程;
的方程;(2)已知
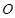 点为原点,连结
点为原点,连结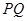 交抛物线
交抛物线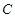 于
于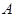 、
、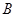 两点,
两点,证明:
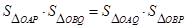 .
.解:(1)如图,设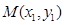 ,
,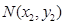

由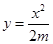 ,得
,得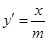 ∴
∴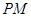 的斜率为
的斜率为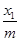
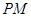 的方程为
的方程为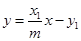 同理得
同理得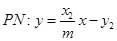
设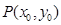 代入上式得
代入上式得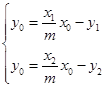 ,
,
即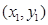 ,
,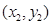 满足方程
满足方程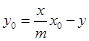
故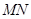 的方程为
的方程为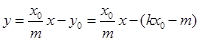 ………………4分
………………4分
上式可化为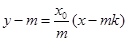 ,过交点
,过交点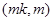
∵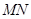 过交点
过交点 , ∴
, ∴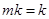 ,
,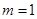
∴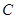 的方程为
的方程为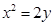 ………………6分
………………6分
(2)要证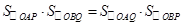 ,即证
,即证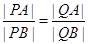
设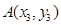 ,
,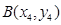
则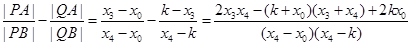 ……(Ⅰ)
……(Ⅰ)
∵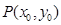 ,
,
∴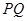 直线方程为
直线方程为 ,
,
与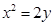 联立化简
联立化简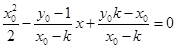
∴ ……①
……①  ……② ……10分
……② ……10分
把①②代入(Ⅰ)式中,则分子
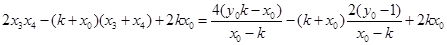
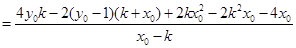 …………(Ⅱ)
…………(Ⅱ)
又 点在直线
点在直线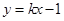 上,∴
上,∴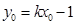 代入Ⅱ中得:
代入Ⅱ中得:
∴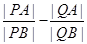
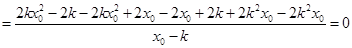
故得证 ………………14分
 ,
,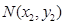

由
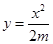 ,得
,得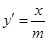 ∴
∴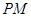 的斜率为
的斜率为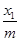
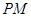 的方程为
的方程为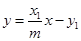 同理得
同理得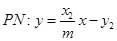
设
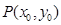 代入上式得
代入上式得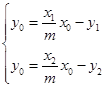 ,
,即
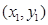 ,
,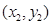 满足方程
满足方程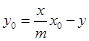
故
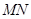 的方程为
的方程为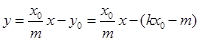 ………………4分
………………4分上式可化为
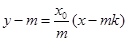 ,过交点
,过交点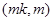
∵
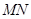 过交点
过交点 , ∴
, ∴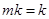 ,
,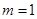
∴
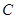 的方程为
的方程为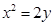 ………………6分
………………6分(2)要证
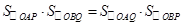 ,即证
,即证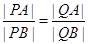
设
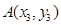 ,
,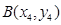
则
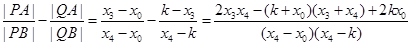 ……(Ⅰ)
……(Ⅰ)∵
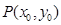 ,
,
∴
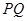 直线方程为
直线方程为 ,
,与
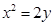 联立化简
联立化简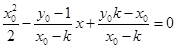
∴
 ……①
……①  ……② ……10分
……② ……10分把①②代入(Ⅰ)式中,则分子
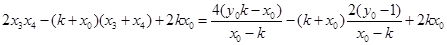
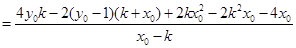 …………(Ⅱ)
…………(Ⅱ)又
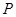 点在直线
点在直线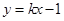 上,∴
上,∴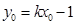 代入Ⅱ中得:
代入Ⅱ中得: ∴
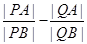
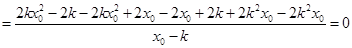
故得证 ………………14分
略

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 的三个顶点在抛物线
的三个顶点在抛物线 :
: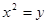 上运动,
上运动, 在坐标原点, 且
在坐标原点, 且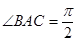 ,点
,点 在
在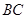 上,且
上,且 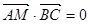 ,
,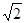 的正三角形
的正三角形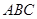 ,若存在,求出这个正三角形
,若存在,求出这个正三角形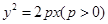 ,当过
,当过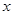 轴上一点
轴上一点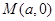 的直线
的直线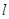 与抛物线交于
与抛物线交于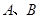 两点时,
两点时,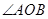 为锐角,则
为锐角,则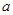 的取值范围 ( )
的取值范围 ( )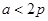
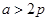
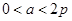
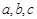 ,则( )
,则( )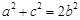
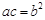
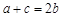
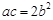

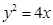 上的一个动点,则点P到点
上的一个动点,则点P到点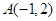 的距离与点P到
的距离与点P到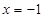 的距离之和的最小值为 .
的距离之和的最小值为 .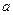 为任何值时,直线
为任何值时,直线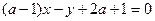 恒过定点P,则过P点的抛物线的标准方程为
恒过定点P,则过P点的抛物线的标准方程为