题目内容
设抛物线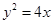 的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使
的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使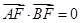 ,则直线AB的斜率
,则直线AB的斜率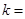 ( )
( )
A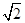 B
B 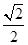 C
C 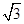 D
D 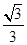
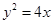 的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使
的焦点为F,过点M(-1,0)的直线在第一象限交抛物线于A、B,使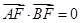 ,则直线AB的斜率
,则直线AB的斜率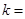 ( )
( )A
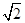 B
B 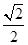 C
C 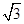 D
D 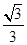
B
本题考查直线和抛物线的综合应用。设直线AB方程为 ,A
,A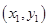 ,B
,B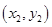 ,由
,由 借助根与系数关系得:
借助根与系数关系得: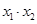 =1,
=1,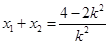 ,又
,又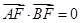 所以
所以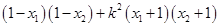 =0,得斜率
=0,得斜率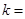
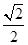
 ,A
,A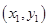 ,B
,B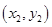 ,由
,由 借助根与系数关系得:
借助根与系数关系得: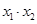 =1,
=1,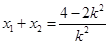 ,又
,又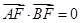 所以
所以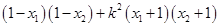 =0,得斜率
=0,得斜率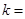

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
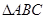 的三个顶点在抛物线
的三个顶点在抛物线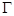 :
: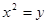 上运动,
上运动,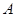 在坐标原点, 且
在坐标原点, 且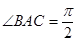 ,点
,点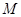 在
在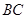 上,且
上,且 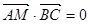 ,
,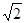 的正三角形
的正三角形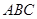 ,若存在,求出这个正三角形
,若存在,求出这个正三角形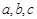 ,则( )
,则( )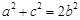
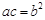
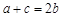
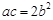

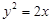 的一条焦点弦,|AB|=4,则AB中点C的横坐标是( )
的一条焦点弦,|AB|=4,则AB中点C的横坐标是( ) 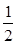
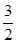
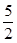
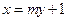 过抛物线
过抛物线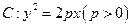 的焦点
的焦点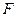 且与抛物线相交于两点
且与抛物线相交于两点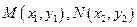 ,自
,自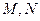 向准线
向准线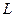 作垂线,垂足分别为
作垂线,垂足分别为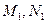 .
.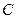 的方程;
的方程;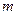 取何实数时,
取何实数时,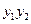 ,
,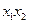 都是定值;
都是定值;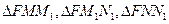 的面积分别为
的面积分别为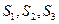 ,试判断
,试判断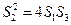 是否成立,并证明你的结论.
是否成立,并证明你的结论.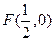 为抛物线
为抛物线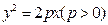 的焦点,点
的焦点,点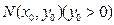 为其上一点,点M与点N关于x轴对称,直线
为其上一点,点M与点N关于x轴对称,直线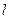 与抛物线交于异于M,N的A,B两点,且
与抛物线交于异于M,N的A,B两点,且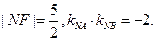
 面积最小的直线
面积最小的直线 ,若存在,求出直线
,若存在,求出直线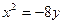 的准线方程为 .
的准线方程为 .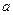 为任何值时,直线
为任何值时,直线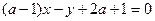 恒过定点P,则过P点的抛物线的标准方程为
恒过定点P,则过P点的抛物线的标准方程为